Quantization Beyond Uniform Bit Allocation

Quantization is a fundamental technique to handle the growing sizes of embeddings generated by modern models. Existing quantization schemes are largely embedding agnostic and allocate bits uniformly across dimensions. However, recent models produce embeddings with significant geometric structure. In this work, we investigate whether a variable bit allocation scheme can improve quantization quality under a fixed memory budget. We propose a simple variable bit allocation framework that partitions an embedding into contiguous buckets and allocates storage non-uniformly across them. Using a greedy allocation strategy, we instantiate this framework for both Product Quantization (PQ) and Scalar Quantization (SQ). We perform a series of experiments on embeddings known to have the Matryoshka property (MRL), and consistently observe that non-uniform allocations outperform uniform baselines at identical storage budgets. The largest improvements occur in the low-bit regime, where uniform allocation is particularly inefficient for MRL embeddings. At the same compression rates, variable allocation improves recall by up to 8\% for PQ and up to 18\% for SQ. Our results suggest a new direction for structure-aware compression and indexing techniques for large-scale retrieval systems.

Query-Limited Community Recovery in Stochastic Block Models

We study exact community recovery in the two-community stochastic block model on $n$ vertices under limited and noisy access to network data. The learner may query a noisy neighborhood oracle that reveals each true neighbor of a queried vertex independently with fixed probability and never returns non-neighbors, subject to a finite query budget. We consider both oracle-only access and a combined model where the learner also observes a single subsampled copy of the underlying graph. For oracle-only access, balanced uniform querying gives a sharp non-adaptive benchmark: when each vertex is queried the same integer number of times, the observations reduce to an SBM with attenuated edge probabilities and the Abbe-Bandeira-Hall exact-recovery threshold applies. We show that this benchmark is not adaptively optimal: a two-stage adaptive strategy succeeds with $n+o(n)$ queries in a regime where balanced uniform querying requires $m n$ queries for some $m>1$. With an additional subsampled graph, we prove a sublinear-query adaptivity gap: balanced data-independent uniform querying with a sublinear budget does not improve over the subsampled graph alone, whereas adaptive querying can target a small set of uncertain vertices and achieve exact recovery. Thus adaptive data acquisition can strictly improve the information-theoretic limits of exact recovery.

Covering a Graph with Dense Subgraph Families, via Triangle-Rich Sets

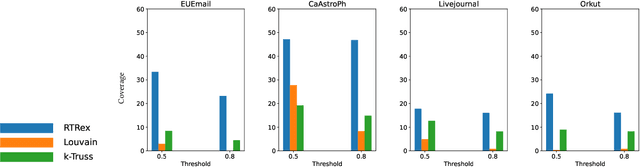
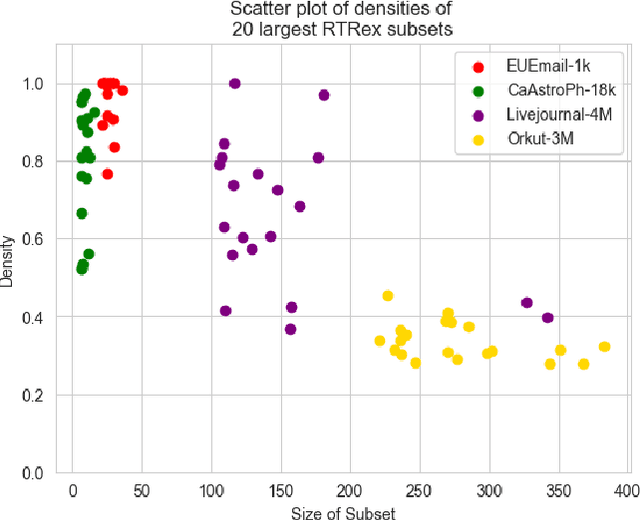
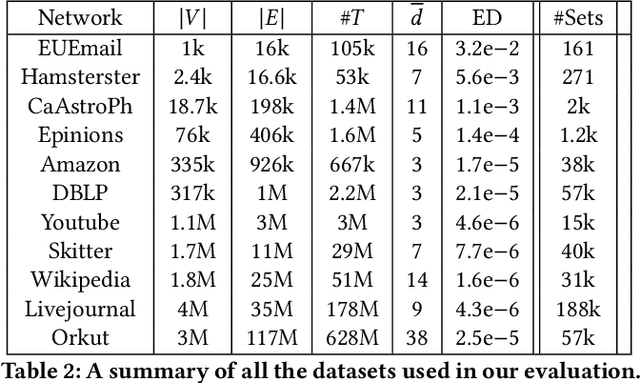
Graphs are a fundamental data structure used to represent relationships in domains as diverse as the social sciences, bioinformatics, cybersecurity, the Internet, and more. One of the central observations in network science is that real-world graphs are globally sparse, yet contains numerous "pockets" of high edge density. A fundamental task in graph mining is to discover these dense subgraphs. Most common formulations of the problem involve finding a single (or a few) "optimally" dense subsets. But in most real applications, one does not care for the optimality. Instead, we want to find a large collection of dense subsets that covers a significant fraction of the input graph. We give a mathematical formulation of this problem, using a new definition of regularly triangle-rich (RTR) families. These families capture the notion of dense subgraphs that contain many triangles and have degrees comparable to the subgraph size. We design a provable algorithm, RTRExtractor, that can discover RTR families that approximately cover any RTR set. The algorithm is efficient and is inspired by recent results that use triangle counts for community testing and clustering. We show that RTRExtractor has excellent behavior on a large variety of real-world datasets. It is able to process graphs with hundreds of millions of edges within minutes. Across many datasets, RTRExtractor achieves high coverage using high edge density datasets. For example, the output covers a quarter of the vertices with subgraphs of edge density more than (say) $0.5$, for datasets with 10M+ edges. We show an example of how the output of RTRExtractor correlates with meaningful sets of similar vertices in a citation network, demonstrating the utility of RTRExtractor for unsupervised graph discovery tasks.