Kernelized Complete Conditional Stein Discrepancy

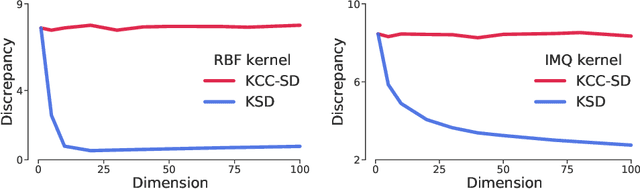
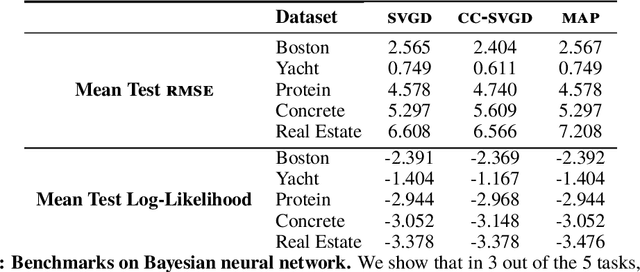
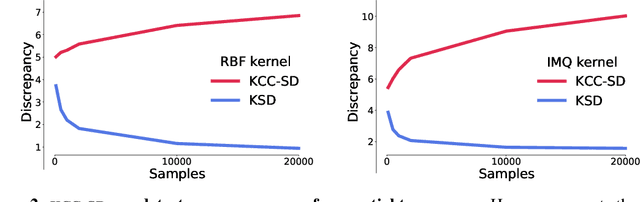
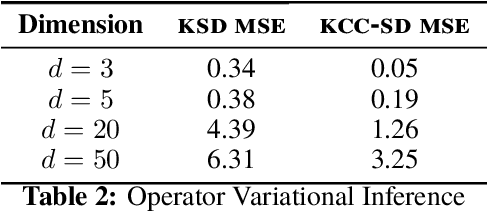
Much of machine learning relies on comparing distributions with discrepancy measures. Stein's method creates discrepancy measures between two distributions that require only the unnormalized density of one and samples from the other. Stein discrepancies can be combined with kernels to define the kernelized Stein discrepancies (KSDs).While kernels make Stein discrepancies tractable, they pose several challenges in high dimensions. We introduce kernelized complete conditional Stein discrepancies (KCC-SDs). Complete conditionals turn a multivariate distribution into multiple univariate distributions. We prove that KCC-SDs detect convergence and non-convergence, and that they upper-bound KSDs. We empirically show that KCC-SDs detect non-convergence where KSDs fail. Our experiments illustrate the difference between KCC-SDs and KSDs when comparing high-dimensional distributions and performing variational inference.