Universal hidden monotonic trend estimation with contrastive learning

In this paper, we describe a universal method for extracting the underlying monotonic trend factor from time series data. We propose an approach related to the Mann-Kendall test, a standard monotonic trend detection method and call it contrastive trend estimation (CTE). We show that the CTE method identifies any hidden trend underlying temporal data while avoiding the standard assumptions used for monotonic trend identification. In particular, CTE can take any type of temporal data (vector, images, graphs, time series, etc.) as input. We finally illustrate the interest of our CTE method through several experiments on different types of data and problems.

Time Series Source Separation with Slow Flows

In this paper, we show that slow feature analysis (SFA), a common time series decomposition method, naturally fits into the flow-based models (FBM) framework, a type of invertible neural latent variable models. Building upon recent advances on blind source separation, we show that such a fit makes the time series decomposition identifiable.

Generalized mean shift with triangular kernel profile

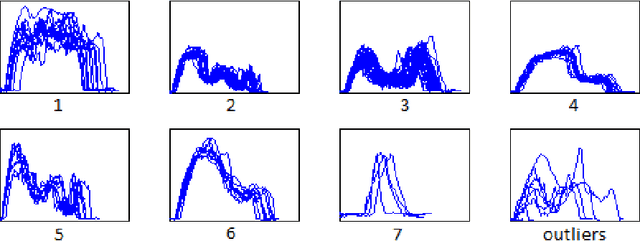
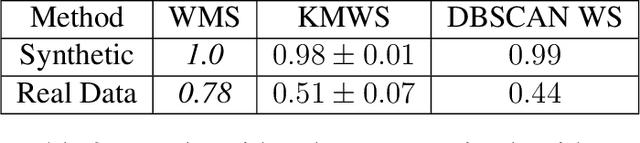
The mean shift algorithm is a popular way to find modes of some probability density functions taking a specific kernel-based shape, used for clustering or visual tracking. Since its introduction, it underwent several practical improvements and generalizations, as well as deep theoretical analysis mainly focused on its convergence properties. In spite of encouraging results, this question has not received a clear general answer yet. In this paper we focus on a specific class of kernels, adapted in particular to the distributions clustering applications which motivated this work. We show that a novel Mean Shift variant adapted to them can be derived, and proved to converge after a finite number of iterations. In order to situate this new class of methods in the general picture of the Mean Shift theory, we alo give a synthetic exposure of existing results of this field.