Multi-Shooting Differential Dynamic Programming for Hybrid Systems using Analytical Derivatives

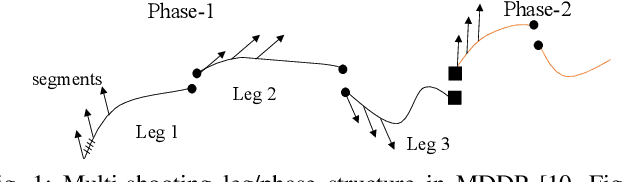
Differential Dynamic Programming (DDP) is a popular technique used to generate motion for dynamic-legged robots in the recent past. However, in most cases, only the first-order partial derivatives of the underlying dynamics are used, resulting in the iLQR approach. Neglecting the second-order terms often slows down the convergence rate compared to full DDP. Multi-Shooting is another popular technique to improve robustness, especially if the dynamics are highly non-linear. In this work, we consider Multi-Shooting DDP for trajectory optimization of a bounding gait for a simplified quadruped model. As the main contribution, we develop Second-Order analytical partial derivatives of the rigid-body contact dynamics, extending our previous results for fixed/floating base models with multi-DoF joints. Finally, we show the benefits of a novel Quasi-Newton method for approximating second-order derivatives of the dynamics, leading to order-of-magnitude speedups in the convergence compared to the full DDP method.

On Second-Order Derivatives of Rigid-Body Dynamics: Theory & Implementation

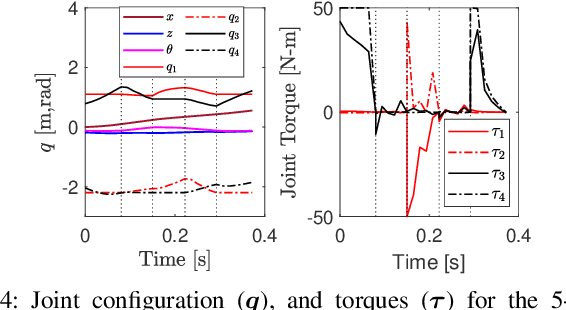
Model-based control for robots has increasingly been dependent on optimization-based methods like Differential Dynamic Programming and iterative LQR (iLQR). These methods can form the basis of Model-Predictive Control (MPC), which is commonly used for controlling legged robots. Computing the partial derivatives of the dynamics is often the most expensive part of these algorithms, regardless of whether analytical methods, Finite Difference, Automatic Differentiation (AD), or Chain-Rule accumulation is used. Since the second-order derivatives of dynamics result in tensor computations, they are often ignored, leading to the use of iLQR, instead of the full second-order DDP method. In this paper, we present analytical methods to compute the second-order derivatives of inverse and forward dynamics for open-chain rigid-body systems with multi-DoF joints and fixed/floating bases. An extensive comparison of accuracy and run-time performance with AD and other methods is provided, including the consideration of code-generation techniques in C/C++ to speed up the computations. For the 36 DoF ATLAS humanoid, the second-order Inverse, and the Forward dynamics derivatives take approx 200 mu s, and approx 2.1 ms respectively, resulting in a 3x speedup over the AD approach.

Closed-Form Second-Order Partial Derivatives of Rigid-Body Inverse Dynamics

Optimization-based control methods for robots often rely on first-order dynamics approximation methods like in iLQR. Using second-order approximations of the dynamics is expensive due to the costly second-order partial derivatives of dynamics with respect to the state and control. Current approaches for calculating these derivatives typically use automatic differentiation (AD) and chain-rule accumulation or finite-difference. In this paper, for the first time, we present closed-form analytical second-order partial derivatives of inverse dynamics for rigid-body systems with floating base and multi-DoF joints. A new extension of spatial vector algebra is proposed that enables the analysis. A recursive $\mathcal{O}(Nd^2)$ algorithm is also provided where $N$ is the number of bodies and $d$ is the depth of the kinematic tree. A comparison with AD in CasADi shows speedups of 1.5-3$\times$ for serial kinematic trees with $N> 5$, and a C++ implementation shows runtimes of $\approx$400$\mu s$ for a quadruped.

Details of Second-Order Partial Derivatives of Rigid-Body Inverse Dynamics

This document provides full details of second-order partial derivatives of rigid-body inverse dynamics. Several properties and identities using an extension of Spatial Vector Algebra for tensorial use are listed, along with their detailed derivations. Using those, the expressions for second-order derivatives are derived step-by-step in detail. The expressions build upon previous work by the authors on first-order partial derivatives of inverse dynamics.

Efficient Analytical Derivatives of Rigid-Body Dynamics using Spatial Vector Algebra

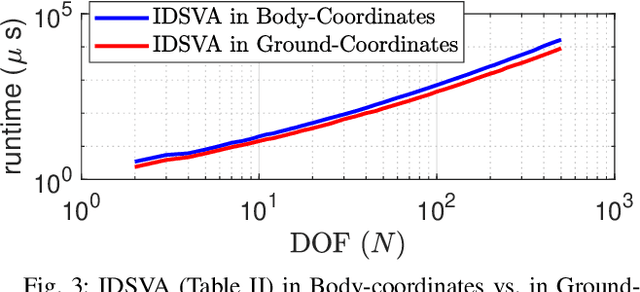
Optimization algorithms are increasingly important for the control of rigid-body systems. An essential requirement for these algorithms is the availability of accurate partial derivatives of the equations of motion with respect to the state and control variables. State of the art methods for calculating the derivatives use analytical differentiation methods based on the chain rule, and although these methods are an improvement over finite-difference in terms of accuracy, they are not always the most efficient. In this paper, we present an analytical method for calculating the first-order partial derivatives of rigid-body dynamics. The method uses Featherstone's spatial vector algebra and is presented in a recursive form similar to the Recursive-Newton Euler Algorithm (RNEA). Several dynamics identities and computational options are exploited for efficiency. The algorithms are bench-marked against competing approaches in Fortran and C++. Timing results are presented for kinematic trees with up to 500 links. As an example, the 100 link case leads to a 7x speedup over our Fortran implementation of the existing state-of-the-art method. Preliminary comparison of compute timings for the partial derivatives of inverse dynamics in C++ are also shown versus the existing Pinocchio framework. A speedup of 1.6x is reported for the 36-dof ATLAS humanoid using the new algorithm proposed in this paper.