Efficient Analytical Derivatives of Rigid-Body Dynamics using Spatial Vector Algebra

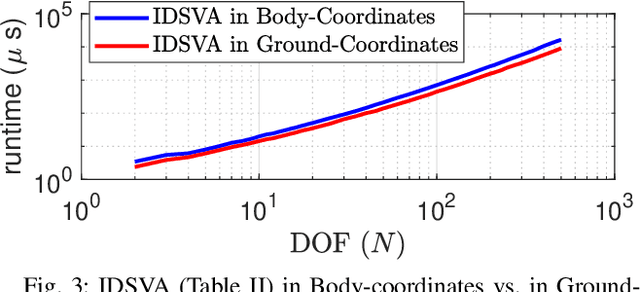
Optimization algorithms are increasingly important for the control of rigid-body systems. An essential requirement for these algorithms is the availability of accurate partial derivatives of the equations of motion with respect to the state and control variables. State of the art methods for calculating the derivatives use analytical differentiation methods based on the chain rule, and although these methods are an improvement over finite-difference in terms of accuracy, they are not always the most efficient. In this paper, we present an analytical method for calculating the first-order partial derivatives of rigid-body dynamics. The method uses Featherstone's spatial vector algebra and is presented in a recursive form similar to the Recursive-Newton Euler Algorithm (RNEA). Several dynamics identities and computational options are exploited for efficiency. The algorithms are bench-marked against competing approaches in Fortran and C++. Timing results are presented for kinematic trees with up to 500 links. As an example, the 100 link case leads to a 7x speedup over our Fortran implementation of the existing state-of-the-art method. Preliminary comparison of compute timings for the partial derivatives of inverse dynamics in C++ are also shown versus the existing Pinocchio framework. A speedup of 1.6x is reported for the 36-dof ATLAS humanoid using the new algorithm proposed in this paper.