Runyu
Cathy
Scalable spectral representations for network multiagent control
Oct 22, 2024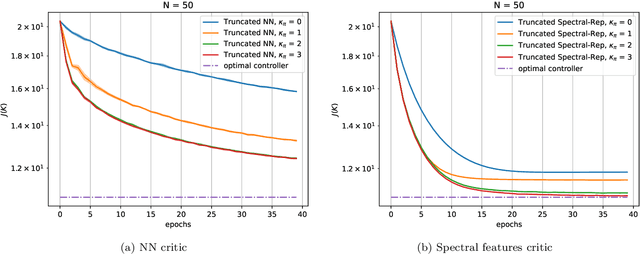
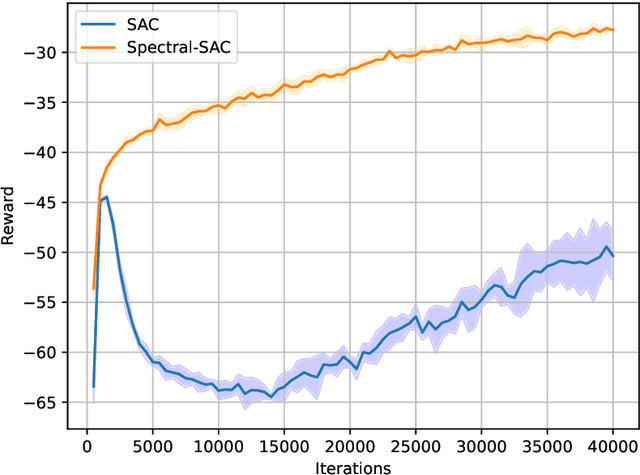
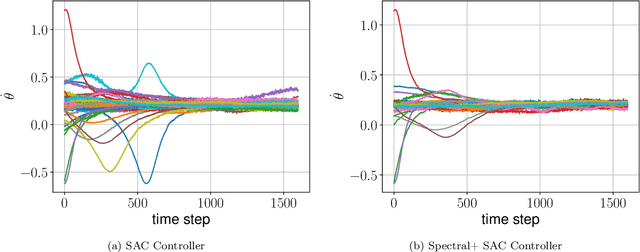
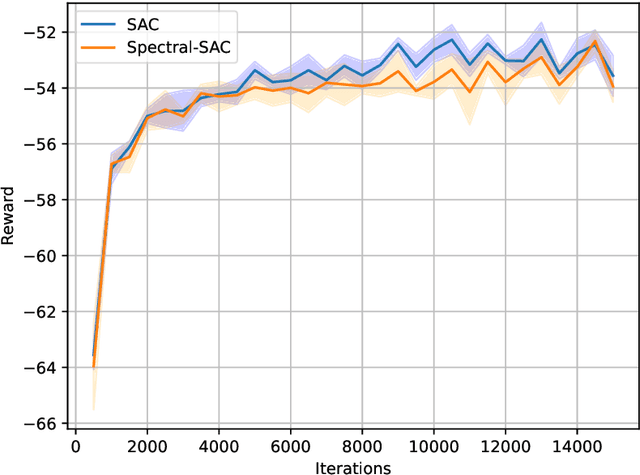
Abstract:Network Markov Decision Processes (MDPs), a popular model for multi-agent control, pose a significant challenge to efficient learning due to the exponential growth of the global state-action space with the number of agents. In this work, utilizing the exponential decay property of network dynamics, we first derive scalable spectral local representations for network MDPs, which induces a network linear subspace for the local $Q$-function of each agent. Building on these local spectral representations, we design a scalable algorithmic framework for continuous state-action network MDPs, and provide end-to-end guarantees for the convergence of our algorithm. Empirically, we validate the effectiveness of our scalable representation-based approach on two benchmark problems, and demonstrate the advantages of our approach over generic function approximation approaches to representing the local $Q$-functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge