Few Batches or Little Memory, But Not Both: Simultaneous Space and Adaptivity Constraints in Stochastic Bandits

We study stochastic multi-armed bandits under simultaneous constraints on space and adaptivity: the learner interacts with the environment in $B$ batches and has only $W$ bits of persistent memory. Prior work shows that each constraint alone is surprisingly mild: near-minimax regret $\widetilde{O}(\sqrt{KT})$ is achievable with $O(\log T)$ bits of memory under fully adaptive interaction, and with a $K$-independent $O(\log\log T)$-type number of batches when memory is unrestricted. We show that this picture breaks down in the simultaneously constrained regime. We prove that any algorithm with a $W$-bit memory constraint must use at least $Ω(K/W)$ batches to achieve near-minimax regret $\widetilde{O}(\sqrt{KT})$ , even under adaptive grids. In particular, logarithmic memory rules out $K$-independent batch complexity. Our proof is based on an information bottleneck. We show that near-minimax regret forces the learner to acquire $Ω(K)$ bits of information about the hidden set of good arms under a suitable hard prior, whereas an algorithm with $B$ batches and $W$ bits of memory allows only $O(BW)$ bits of information. A key ingredient is a localized change-of-measure lemma that yields probability-level arm exploration guarantees, which is of independent interest. We also give an algorithm using $O(\log T)$ bits of memory and $\widetilde{O}(K)$ batches that achieves regret $\widetilde{O}(\sqrt{KT})$, which nearly matches our lower bound.

Kimi K2.5: Visual Agentic Intelligence

We introduce Kimi K2.5, an open-source multimodal agentic model designed to advance general agentic intelligence. K2.5 emphasizes the joint optimization of text and vision so that two modalities enhance each other. This includes a series of techniques such as joint text-vision pre-training, zero-vision SFT, and joint text-vision reinforcement learning. Building on this multimodal foundation, K2.5 introduces Agent Swarm, a self-directed parallel agent orchestration framework that dynamically decomposes complex tasks into heterogeneous sub-problems and executes them concurrently. Extensive evaluations show that Kimi K2.5 achieves state-of-the-art results across various domains including coding, vision, reasoning, and agentic tasks. Agent Swarm also reduces latency by up to $4.5\times$ over single-agent baselines. We release the post-trained Kimi K2.5 model checkpoint to facilitate future research and real-world applications of agentic intelligence.

EvolProver: Advancing Automated Theorem Proving by Evolving Formalized Problems via Symmetry and Difficulty

Large Language Models (LLMs) for formal theorem proving have shown significant promise, yet they often lack generalizability and are fragile to even minor transformations of problem statements. To address this limitation, we introduce a novel data augmentation pipeline designed to enhance model robustness from two perspectives: symmetry and difficulty. From the symmetry perspective, we propose two complementary methods: EvolAST, an Abstract Syntax Tree (AST) based approach that targets syntactic symmetry to generate semantically equivalent problem variants, and EvolDomain, which leverages LLMs to address semantic symmetry by translating theorems across mathematical domains. From the difficulty perspective, we propose EvolDifficulty, which uses carefully designed evolutionary instructions to guide LLMs in generating new theorems with a wider range of difficulty. We then use the evolved data to train EvolProver, a 7B-parameter non-reasoning theorem prover. EvolProver establishes a new state-of-the-art (SOTA) on FormalMATH-Lite with a 53.8% pass@32 rate, surpassing all models of comparable size, including reasoning-based models. It also sets new SOTA records for non-reasoning models on MiniF2F-Test (69.8% pass@32), Ineq-Comp-Seed (52.2% pass@32), and Ineq-Comp-Transformed (34.0% pass@32). Ablation studies further confirm our data augmentation pipeline's effectiveness across multiple benchmarks.

Nearly Tight Bounds for Cross-Learning Contextual Bandits with Graphical Feedback

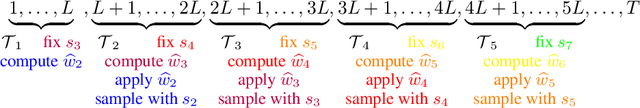
The cross-learning contextual bandit problem with graphical feedback has recently attracted significant attention. In this setting, there is a contextual bandit with a feedback graph over the arms, and pulling an arm reveals the loss for all neighboring arms in the feedback graph across all contexts. Initially proposed by Han et al. (2024), this problem has broad applications in areas such as bidding in first price auctions, and explores a novel frontier in the feedback structure of bandit problems. A key theoretical question is whether an algorithm with $\widetilde{O}(\sqrt{\alpha T})$ regret exists, where $\alpha$ represents the independence number of the feedback graph. This question is particularly interesting because it concerns whether an algorithm can achieve a regret bound entirely independent of the number of contexts and matching the minimax regret of vanilla graphical bandits. Previous work has demonstrated that such an algorithm is impossible for adversarial contexts, but the question remains open for stochastic contexts. In this work, we affirmatively answer this open question by presenting an algorithm that achieves the minimax $\widetilde{O}(\sqrt{\alpha T})$ regret for cross-learning contextual bandits with graphical feedback and stochastic contexts. Notably, although that question is open even for stochastic bandits, we directly solve the strictly stronger adversarial bandit version of the problem.

High Probability Bound for Cross-Learning Contextual Bandits with Unknown Context Distributions

Motivated by applications in online bidding and sleeping bandits, we examine the problem of contextual bandits with cross learning, where the learner observes the loss associated with the action across all possible contexts, not just the current round's context. Our focus is on a setting where losses are chosen adversarially, and contexts are sampled i.i.d. from a specific distribution. This problem was first studied by Balseiro et al. (2019), who proposed an algorithm that achieves near-optimal regret under the assumption that the context distribution is known in advance. However, this assumption is often unrealistic. To address this issue, Schneider and Zimmert (2023) recently proposed a new algorithm that achieves nearly optimal expected regret. It is well-known that expected regret can be significantly weaker than high-probability bounds. In this paper, we present a novel, in-depth analysis of their algorithm and demonstrate that it actually achieves near-optimal regret with high probability. There are steps in the original analysis by Schneider and Zimmert (2023) that lead only to an expected bound by nature. In our analysis, we introduce several new insights. Specifically, we make extensive use of the weak dependency structure between different epochs, which was overlooked in previous analyses. Additionally, standard martingale inequalities are not directly applicable, so we refine martingale inequalities to complete our analysis.