Ruiliang Bai
Deep Learning Guided Undersampling Mask Design for MR Image Reconstruction
Mar 08, 2020
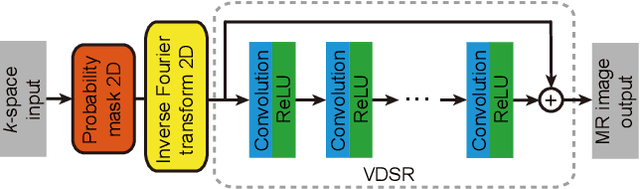
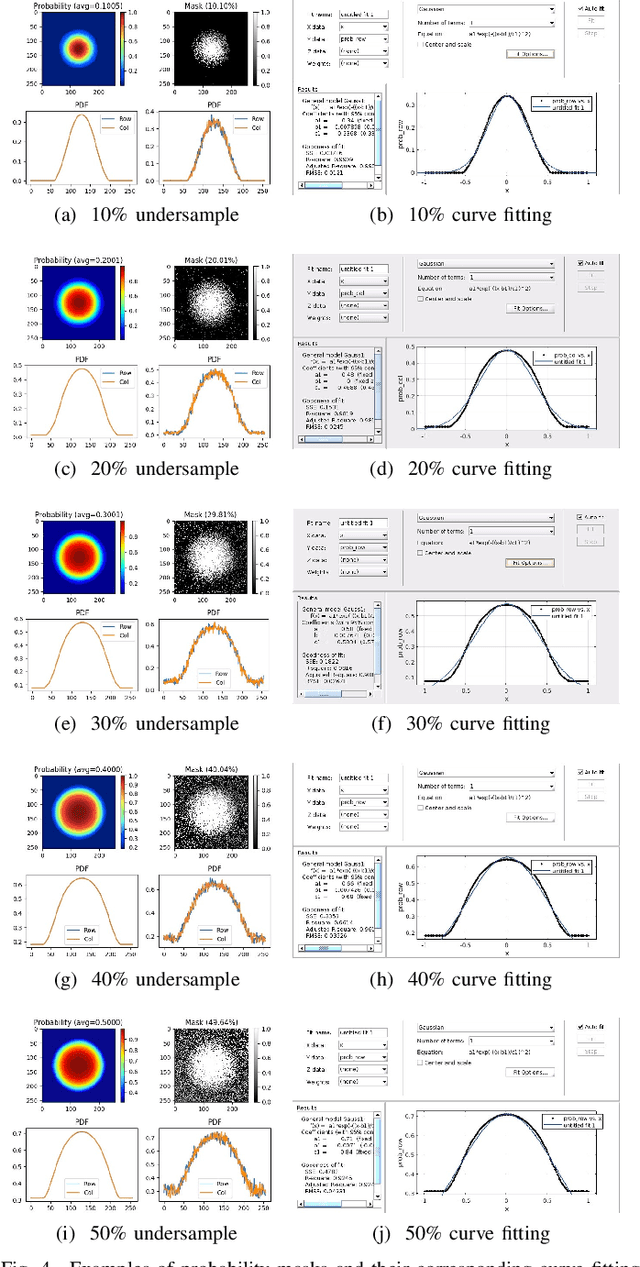
Abstract:In this paper, we propose a cross-domain networks that can achieve undersampled MR image reconstruction from raw k-space space. We design a 2D probability sampling mask layer to simulate real undersampling operation. Then the 2D Inverse FFT is deployed to reconstruct MR image from frequency domain to spatial domain. By minimizing the Euclidean loss between ground-truth image and output, we train the parameters in our probability mask layer. We discover the probability appears special patterns that is quite different from universal common sense that mask should be Poisson-like, under certain undersampled rates. We analyze the probability mask is subjected to Gaussian or Quadratic distributions, and discuss this pattern will be more accurate and robust than traditional ones. Extensive experiments proves that the rules we discovered are adaptive to most cases. This can be a useful guidance to further MR reconstruction mask designs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge