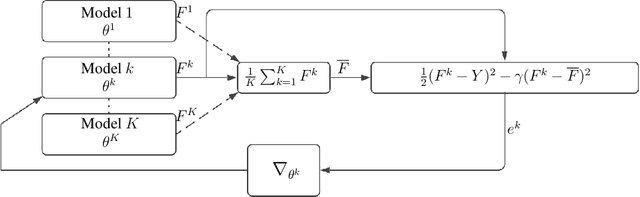
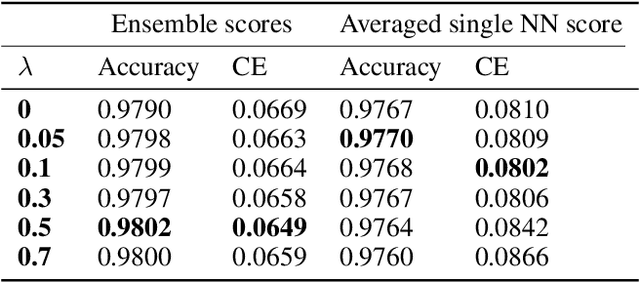
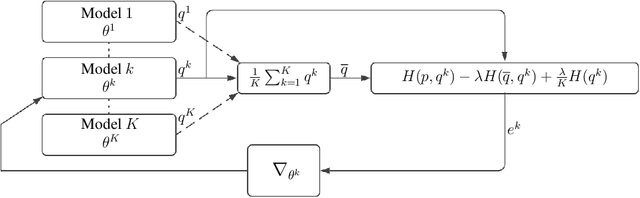
Amended Cross Entropy Cost: Framework For Explicit Diversity Encouragement

Cross Entropy (CE) has an important role in machine learning and, in particular, in neural networks. It is commonly used in neural networks as the cost between the known distribution of the label and the Softmax/Sigmoid output. In this paper we present a new cost function called the Amended Cross Entropy (ACE). Its novelty lies in its affording the capability to train multiple classifiers while explicitly controlling the diversity between them. We derived the new cost by mathematical analysis and "reverse engineering" of the way we wish the gradients to behave, and produced a tailor-made, elegant and intuitive cost function to achieve the desired result. This process is similar to the way that CE cost is picked as a cost function for the Softmax/Sigmoid classifiers for obtaining linear derivatives. By choosing the optimal diversity factor we produce an ensemble which yields better results than the vanilla one. We demonstrate two potential usages of this outcome, and present empirical results. Our method works for classification problems analogously to Negative Correlation Learning (NCL) for regression problems.

Highway State Gating for Recurrent Highway Networks: improving information flow through time

Recurrent Neural Networks (RNNs) play a major role in the field of sequential learning, and have outperformed traditional algorithms on many benchmarks. Training deep RNNs still remains a challenge, and most of the state-of-the-art models are structured with a transition depth of 2-4 layers. Recurrent Highway Networks (RHNs) were introduced in order to tackle this issue. These have achieved state-of-the-art performance on a few benchmarks using a depth of 10 layers. However, the performance of this architecture suffers from a bottleneck, and ceases to improve when an attempt is made to add more layers. In this work, we analyze the causes for this, and postulate that the main source is the way that the information flows through time. We introduce a novel and simple variation for the RHN cell, called Highway State Gating (HSG), which allows adding more layers, while continuing to improve performance. By using a gating mechanism for the state, we allow the net to "choose" whether to pass information directly through time, or to gate it. This mechanism also allows the gradient to back-propagate directly through time and, therefore, results in a slightly faster convergence. We use the Penn Treebank (PTB) dataset as a platform for empirical proof of concept. Empirical results show that the improvement due to Highway State Gating is for all depths, and as the depth increases, the improvement also increases.