Utility Inspired Generalizations of TOPSIS

TOPSIS, a popular method for ranking alternatives is based on aggregated distances to ideal and anti-ideal points. As such, it was considered to be essentially different from widely popular and acknowledged `utility-based methods', which build rankings from weight-averaged utility values. Nonetheless, TOPSIS has recently been shown to be a natural generalization of these `utility-based methods' on the grounds that the distances it uses can be decomposed into so called weight-scaled means (WM) and weight-scaled standard deviations (WSD) of utilities. However, the influence that these two components exert on the final ranking cannot be in any way influenced in the standard TOPSIS. This is why, building on our previous results, in this paper we put forward modifications that make TOPSIS aggregations responsive to WM and WSD, achieving some amount of well interpretable control over how the rankings are influenced by WM and WSD. The modifications constitute a natural generalization of the standard TOPSIS method because, thanks to them, the generalized TOPSIS may turn into the original TOPSIS or, otherwise, following the decision maker's preferences, may trade off WM for WSD or WSD for WM. In the latter case, TOPSIS gradually reduces to a regular `utility-based method'. All in all, we believe that the proposed generalizations constitute an interesting practical tool for influencing the ranking by controlled application of a new form of decision maker's preferences.

Properties of fairness measures in the context of varying class imbalance and protected group ratios

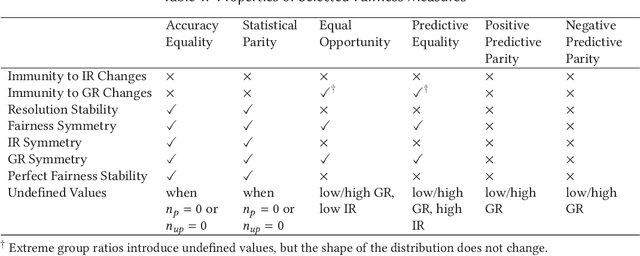
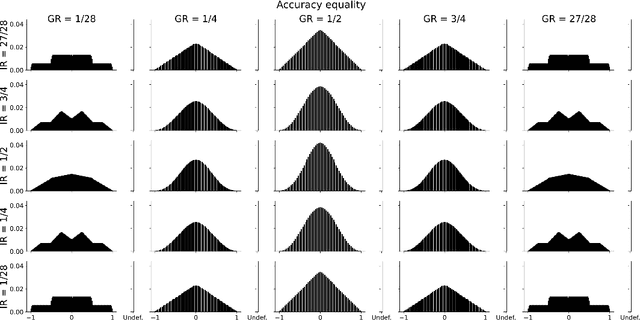
Society is increasingly relying on predictive models in fields like criminal justice, credit risk management, or hiring. To prevent such automated systems from discriminating against people belonging to certain groups, fairness measures have become a crucial component in socially relevant applications of machine learning. However, existing fairness measures have been designed to assess the bias between predictions for protected groups without considering the imbalance in the classes of the target variable. Current research on the potential effect of class imbalance on fairness focuses on practical applications rather than dataset-independent measure properties. In this paper, we study the general properties of fairness measures for changing class and protected group proportions. For this purpose, we analyze the probability mass functions of six of the most popular group fairness measures. We also measure how the probability of achieving perfect fairness changes for varying class imbalance ratios. Moreover, we relate the dataset-independent properties of fairness measures described in this paper to classifier fairness in real-life tasks. Our results show that measures such as Equal Opportunity and Positive Predictive Parity are more sensitive to changes in class imbalance than Accuracy Equality. These findings can help guide researchers and practitioners in choosing the most appropriate fairness measures for their classification problems.

Towards Explainable TOPSIS: Visual Insights into the Effects of Weights and Aggregations on Rankings

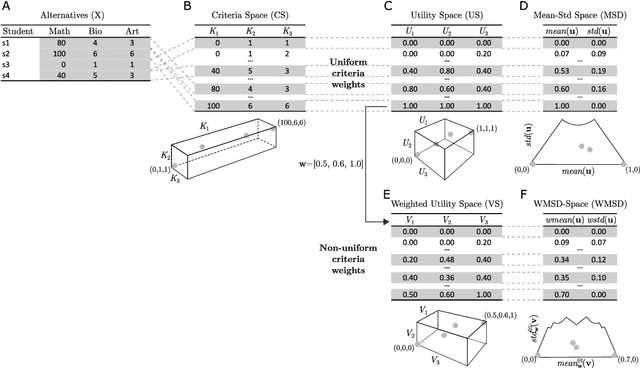
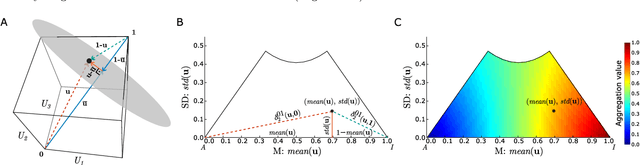
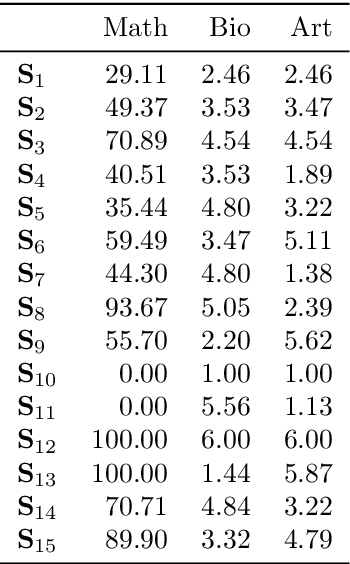
Multi-Criteria Decision Analysis (MCDA) is extensively used across diverse industries to assess and rank alternatives. Among numerous MCDA methods developed to solve real-world ranking problems, TOPSIS remains one of the most popular choices in many application areas. TOPSIS calculates distances between the considered alternatives and two predefined ones, namely the ideal and the anti-ideal, and creates a ranking of the alternatives according to a chosen aggregation of these distances. However, the interpretation of the inner workings of TOPSIS is difficult, especially when the number of criteria is large. To this end, recent research has shown that TOPSIS aggregations can be expressed using the means (M) and standard deviations (SD) of alternatives, creating MSD-space, a tool for visualizing and explaining aggregations. Even though MSD-space is highly useful, it assumes equally important criteria, making it less applicable to real-world ranking problems. In this paper, we generalize the concept of MSD-space to weighted criteria by introducing the concept of WMSD-space defined by what is referred to as weight-scaled means and standard deviations. We demonstrate that TOPSIS and similar distance-based aggregation methods can be successfully illustrated in a plane and interpreted even when the criteria are weighted, regardless of their number. The proposed WMSD-space offers a practical method for explaining TOPSIS rankings in real-world decision problems.