Oja's plasticity rule overcomes several challenges of training neural networks under biological constraints

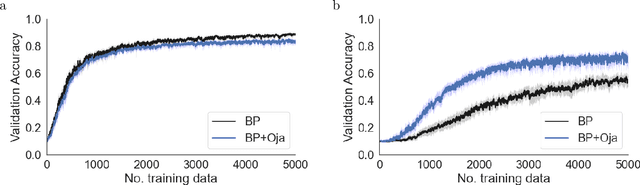
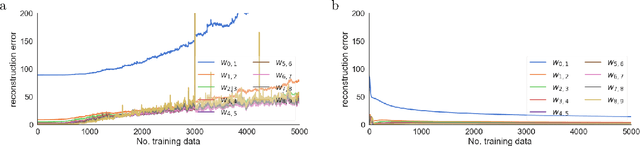
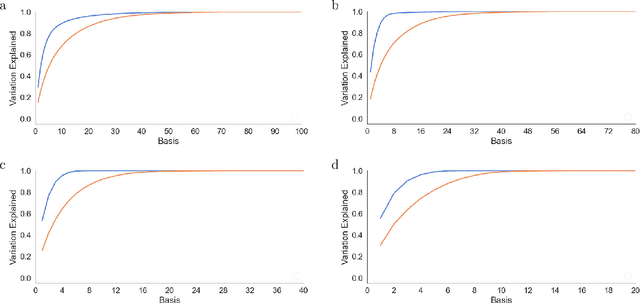
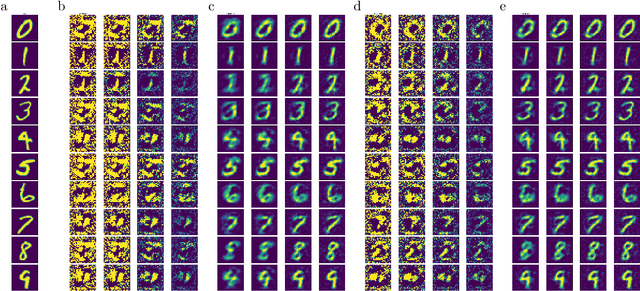
There is a large literature on the similarities and differences between biological neural circuits and deep artificial neural networks (DNNs). However, modern training of DNNs relies on several engineering tricks such as data batching, normalization, adaptive optimizers, and precise weight initialization. Despite their critical role in training DNNs, these engineering tricks are often overlooked when drawing parallels between biological and artificial networks, potentially due to a lack of evidence for their direct biological implementation. In this study, we show that Oja's plasticity rule partly overcomes the need for some engineering tricks. Specifically, under difficult, but biologically realistic learning scenarios such as online learning, deep architectures, and sub-optimal weight initialization, Oja's rule can substantially improve the performance of pure backpropagation. Our results demonstrate that simple synaptic plasticity rules can overcome challenges to learning that are typically overcome using less biologically plausible approaches when training DNNs.

Learning fixed points of recurrent neural networks by reparameterizing the network model

In computational neuroscience, fixed points of recurrent neural networks are commonly used to model neural responses to static or slowly changing stimuli. These applications raise the question of how to train the weights in a recurrent neural network to minimize a loss function evaluated on fixed points. A natural approach is to use gradient descent on the Euclidean space of synaptic weights. We show that this approach can lead to poor learning performance due, in part, to singularities that arise in the loss surface. We use a reparameterization of the recurrent network model to derive two alternative learning rules that produces more robust learning dynamics. We show that these learning rules can be interpreted as steepest descent and gradient descent, respectively, under a non-Euclidean metric on the space of recurrent weights. Our results question the common, implicit assumption that learning in the brain should be expected to follow the negative Euclidean gradient of synaptic weights.

Meta-Learning Biologically Plausible Plasticity Rules with Random Feedback Pathways

Backpropagation is widely used to train artificial neural networks, but its relationship to synaptic plasticity in the brain is unknown. Some biological models of backpropagation rely on feedback projections that are symmetric with feedforward connections, but experiments do not corroborate the existence of such symmetric backward connectivity. Random feedback alignment offers an alternative model in which errors are propagated backward through fixed, random backward connections. This approach successfully trains shallow models, but learns slowly and does not perform well with deeper models or online learning. In this study, we develop a novel meta-plasticity approach to discover interpretable, biologically plausible plasticity rules that improve online learning performance with fixed random feedback connections. The resulting plasticity rules show improved online training of deep models in the low data regime. Our results highlight the potential of meta-plasticity to discover effective, interpretable learning rules satisfying biological constraints.

On the relationship between predictive coding and backpropagation

Artificial neural networks are often interpreted as abstract models of biological neuronal networks, but they are typically trained using the biologically unrealistic backpropagation algorithm and its variants. Predictive coding has been offered as a potentially more biologically realistic alternative to backpropagation for training neural networks. In this manuscript, I review and extend recent work on the mathematical relationship between predictive coding and backpropagation for training feedforward artificial neural networks on supervised learning tasks. I discuss some implications of these results for the interpretation of predictive coding and deep neural networks as models of biological learning and I describe a repository of functions, Torch2PC, for performing predictive coding with PyTorch neural network models.

A model of reward-modulated motor learning with parallelcortical and basal ganglia pathways

Many recent studies of the motor system are divided into two distinct approaches: Those that investigate how motor responses are encoded in cortical neurons' firing rate dynamics and those that study the learning rules by which mammals and songbirds develop reliable motor responses. Computationally, the first approach is encapsulated by reservoir computing models, which can learn intricate motor tasks and produce internal dynamics strikingly similar to those of motor cortical neurons, but rely on biologically unrealistic learning rules. The more realistic learning rules developed by the second approach are often derived for simplified, discrete tasks in contrast to the intricate dynamics that characterize real motor responses. We bridge these two approaches to develop a biologically realistic learning rule for reservoir computing. Our algorithm learns simulated motor tasks on which previous reservoir computing algorithms fail, and reproduces experimental findings including those that relate motor learning to Parkinson's disease and its treatment.