On the Validity of Conformal Prediction for Network Data Under Non-Uniform Sampling

We study the properties of conformal prediction for network data under various sampling mechanisms that commonly arise in practice but often result in a non-representative sample of nodes. We interpret these sampling mechanisms as selection rules applied to a superpopulation and study the validity of conformal prediction conditional on an appropriate selection event. We show that the sampled subarray is exchangeable conditional on the selection event if the selection rule satisfies a permutation invariance property and a joint exchangeability condition holds for the superpopulation. Our result implies the finite-sample validity of conformal prediction for certain selection events related to ego networks and snowball sampling. We also show that when data are sampled via a random walk on a graph, a variant of weighted conformal prediction yields asymptotically valid prediction sets for an independently selected node from the population.

Conformal Prediction for Network-Assisted Regression

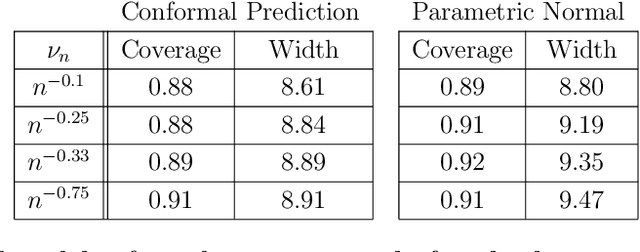
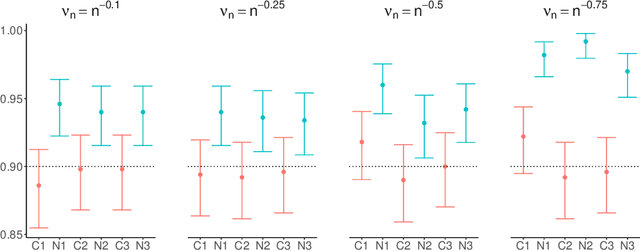
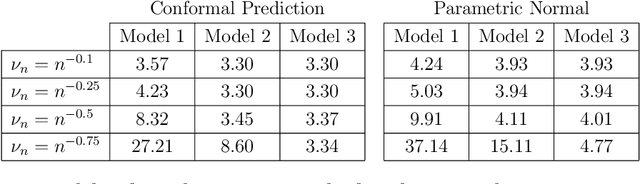
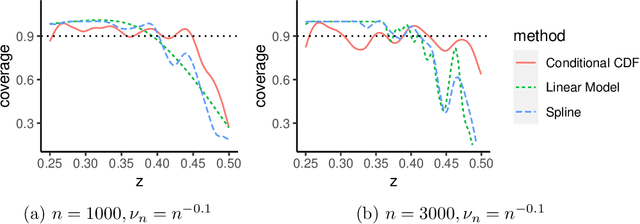
An important problem in network analysis is predicting a node attribute using both network covariates, such as graph embedding coordinates or local subgraph counts, and conventional node covariates, such as demographic characteristics. While standard regression methods that make use of both types of covariates may be used for prediction, statistical inference is complicated by the fact that the nodal summary statistics are often dependent in complex ways. We show that under a mild joint exchangeability assumption, a network analog of conformal prediction achieves finite sample validity for a wide range of network covariates. We also show that a form of asymptotic conditional validity is achievable. The methods are illustrated on both simulated networks and a citation network dataset.

Bootstrapping the error of Oja's Algorithm

We consider the problem of quantifying uncertainty for the estimation error of the leading eigenvector from Oja's algorithm for streaming principal component analysis, where the data are generated IID from some unknown distribution. By combining classical tools from the U-statistics literature with recent results on high-dimensional central limit theorems for quadratic forms of random vectors and concentration of matrix products, we establish a $\chi^2$ approximation result for the $\sin^2$ error between the population eigenvector and the output of Oja's algorithm. Since estimating the covariance matrix associated with the approximating distribution requires knowledge of unknown model parameters, we propose a multiplier bootstrap algorithm that may be updated in an online manner. We establish conditions under which the bootstrap distribution is close to the corresponding sampling distribution with high probability, thereby establishing the bootstrap as a consistent inferential method in an appropriate asymptotic regime.

Higher-Order Correct Multiplier Bootstraps for Count Functionals of Networks

Subgraph counts play a central role in both graph limit theory and network data analysis. In recent years, substantial progress has been made in the area of uncertainty quantification for these functionals; several procedures are now known to be consistent for the problem. In this paper, we propose a new class of multiplier bootstraps for count functionals. We show that a bootstrap procedure with a multiplicative weights exhibits higher-order correctness under appropriate sparsity conditions. Since this bootstrap is computationally expensive, we propose linear and quadratic approximations to the multiplier bootstrap, which correspond to the first and second-order Hayek projections of an approximating U-statistic, respectively. We show that the quadratic bootstrap procedure achieves higher-order correctness under analogous conditions to the multiplicative bootstrap while having much better computational properties. We complement our theoretical results with a simulation study and verify that our procedure offers state-of-the-art performance for several functionals.

On the Theoretical Properties of the Network Jackknife

We study the properties of a leave-node-out jackknife procedure for network data. Under the sparse graphon model, we prove an Efron-Stein-type inequality, showing that the network jackknife leads to conservative estimates of the variance (in expectation) for any network functional that is invariant to node permutation. For a general class of count functionals, we also establish consistency of the network jackknife. We complement our theoretical analysis with a range of simulated and real-data examples and show that the network jackknife offers competitive performance in cases where other resampling methods are known to be valid. In fact, for several network statistics, we see that the jackknife provides more accurate inferences compared to related methods such as subsampling.