Sparse Autoencoders Find Highly Interpretable Features in Language Models

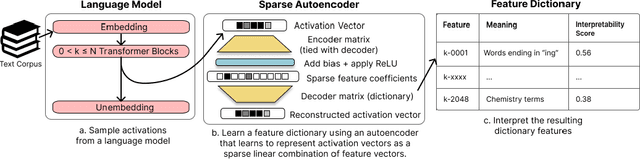
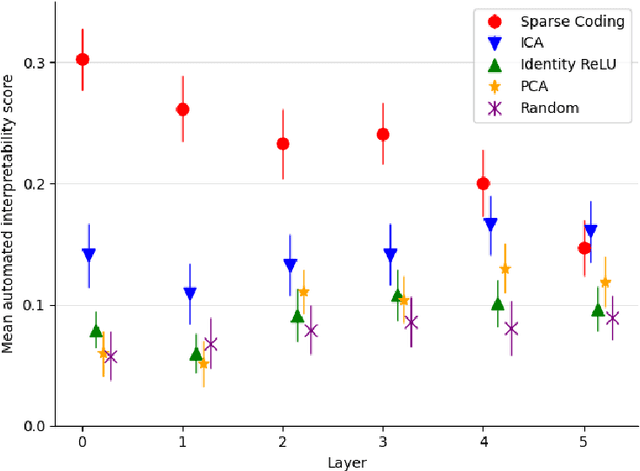
One of the roadblocks to a better understanding of neural networks' internals is \textit{polysemanticity}, where neurons appear to activate in multiple, semantically distinct contexts. Polysemanticity prevents us from identifying concise, human-understandable explanations for what neural networks are doing internally. One hypothesised cause of polysemanticity is \textit{superposition}, where neural networks represent more features than they have neurons by assigning features to an overcomplete set of directions in activation space, rather than to individual neurons. Here, we attempt to identify those directions, using sparse autoencoders to reconstruct the internal activations of a language model. These autoencoders learn sets of sparsely activating features that are more interpretable and monosemantic than directions identified by alternative approaches, where interpretability is measured by automated methods. Ablating these features enables precise model editing, for example, by removing capabilities such as pronoun prediction, while disrupting model behaviour less than prior techniques. This work indicates that it is possible to resolve superposition in language models using a scalable, unsupervised method. Our method may serve as a foundation for future mechanistic interpretability work, which we hope will enable greater model transparency and steerability.

Attention-Only Transformers and Implementing MLPs with Attention Heads

The transformer architecture is widely used in machine learning models and consists of two alternating sublayers: attention heads and MLPs. We prove that an MLP neuron can be implemented by a masked attention head with internal dimension 1 so long as the MLP's activation function comes from a restricted class including SiLU and close approximations of ReLU and GeLU. This allows one to convert an MLP-and-attention transformer into an attention-only transformer at the cost of greatly increasing the number of attention heads. We also prove that attention heads can perform the components of an MLP (linear transformations and activation functions) separately. Finally, we prove that attention heads can encode arbitrary masking patterns in their weight matrices to within arbitrarily small error.