Evaluating Neighbor Explainability for Graph Neural Networks

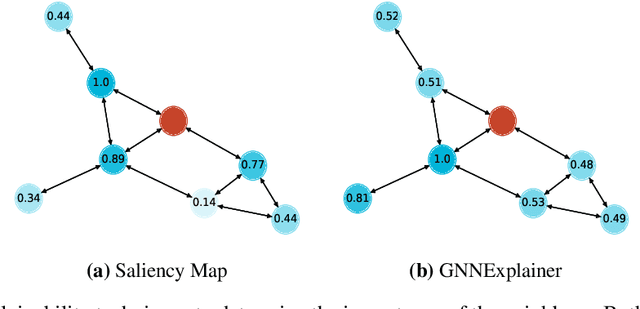
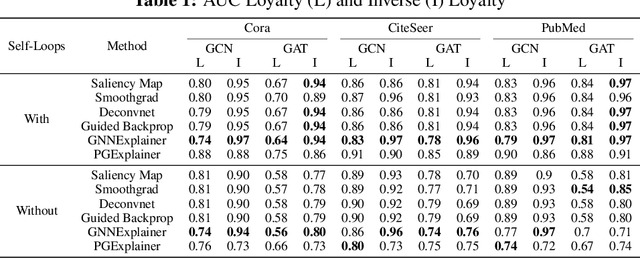
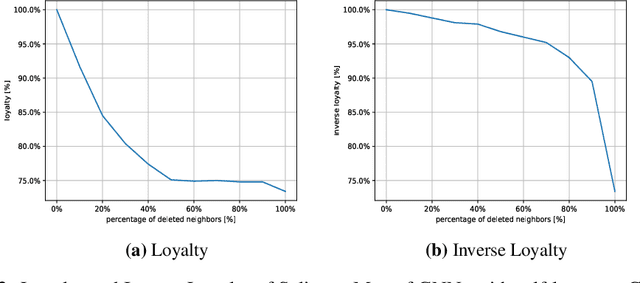
Explainability in Graph Neural Networks (GNNs) is a new field growing in the last few years. In this publication we address the problem of determining how important is each neighbor for the GNN when classifying a node and how to measure the performance for this specific task. To do this, various known explainability methods are reformulated to get the neighbor importance and four new metrics are presented. Our results show that there is almost no difference between the explanations provided by gradient-based techniques in the GNN domain. In addition, many explainability techniques failed to identify important neighbors when GNNs without self-loops are used.

Vaccine skepticism detection by network embedding

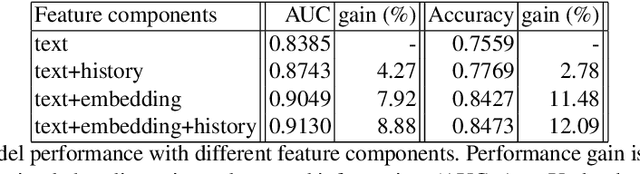
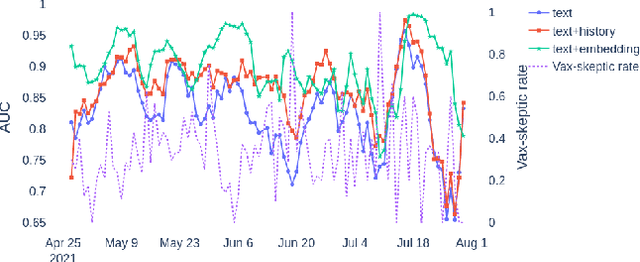
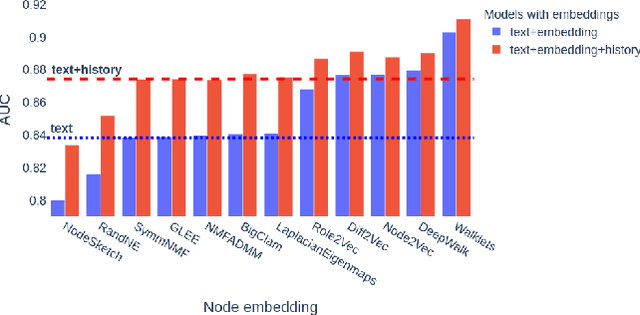
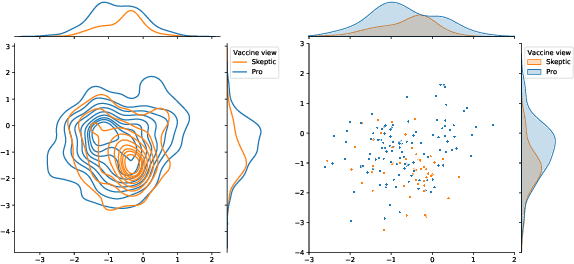
We demonstrate the applicability of network embedding to vaccine skepticism, a controversial topic of long-past history. With the Covid-19 pandemic outbreak at the end of 2019, the topic is more important than ever. Only a year after the first international cases were registered, multiple vaccines were developed and passed clinical testing. Besides the challenges of development, testing, and logistics, another factor that might play a significant role in the fight against the pandemic are people who are hesitant to get vaccinated, or even state that they will refuse any vaccine offered to them. Two groups of people commonly referred to as a) pro-vaxxer, those who support vaccinating people b) vax-skeptic, those who question vaccine efficacy or the need for general vaccination against Covid-19. It is very difficult to tell exactly how many people share each of these views. It is even more difficult to understand all the reasoning why vax-skeptic opinions are getting more popular. In this work, our intention was to develop techniques that are able to efficiently differentiate between pro-vaxxer and vax-skeptic content. After multiple data preprocessing steps, we analyzed the tweet text as well as the structure of user interactions on Twitter. We deployed several node embedding and community detection models that scale well for graphs with millions of edges.