Towards Arbitrary QUBO Optimization: Analysis of Classical and Quantum-Activated Feedforward Neural Networks

Quadratic Unconstrained Binary Optimization (QUBO) sits at the heart of many industries and academic fields such as logistics, supply chain, finance, pharmaceutical science, chemistry, IT, and energy sectors, among others. These problems typically involve optimizing a large number of binary variables, which makes finding exact solutions exponentially more difficult. Consequently, most QUBO problems are classified as NP-hard. To address this challenge, we developed a powerful feedforward neural network (FNN) optimizer for arbitrary QUBO problems. In this work, we demonstrate that the FNN optimizer can provide high-quality approximate solutions for large problems, including dense 80-variable weighted MaxCut and random QUBOs, achieving an average accuracy of over 99% in less than 1.1 seconds on an 8-core CPU. Additionally, the FNN optimizer outperformed the Gurobi optimizer by 72% on 200-variable random QUBO problems within a 100-second computation time limit, exhibiting strong potential for real-time optimization tasks. Building on this model, we explored the novel approach of integrating FNNs with a quantum annealer-based activation function to create a quantum-classical encoder-decoder (QCED) optimizer, aiming to further enhance the performance of FNNs in QUBO optimization.

Bayesian optimal control of GHZ states in Rydberg lattices

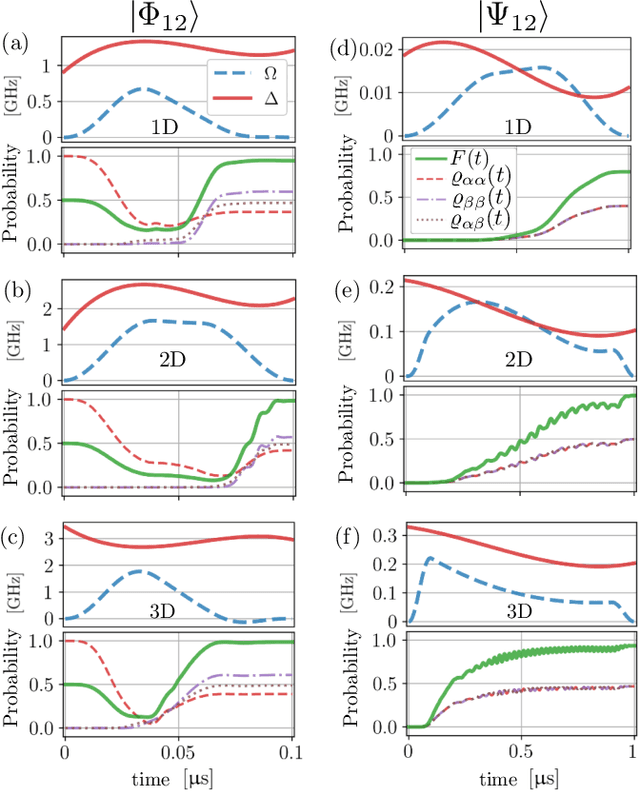
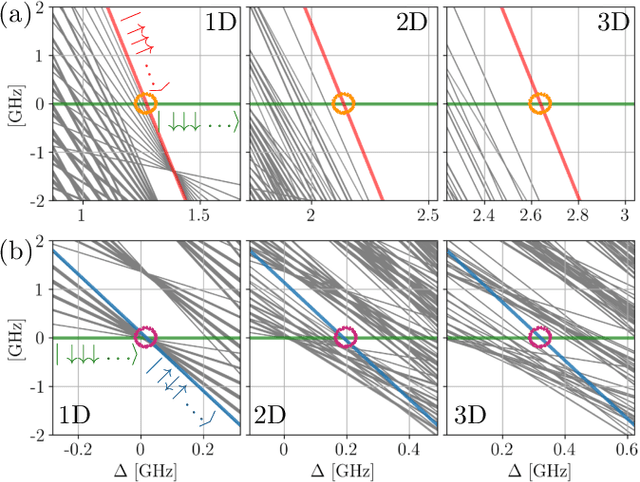
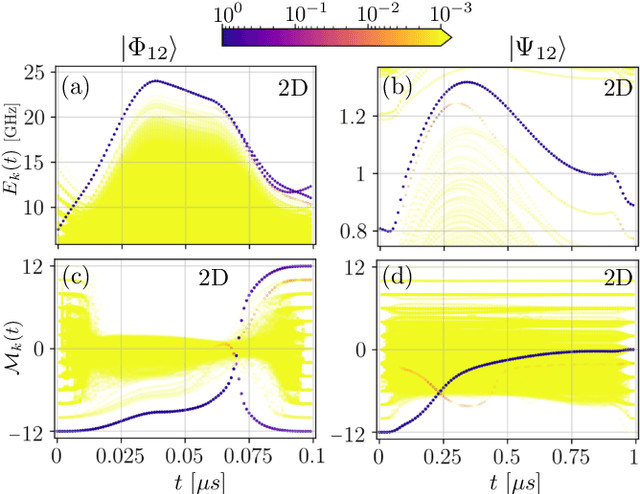
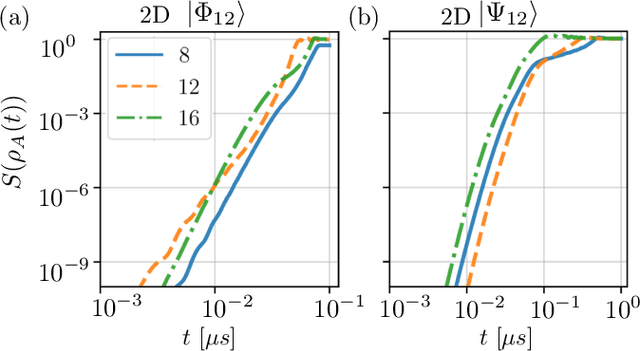
The ability to prepare non-classical states in a robust manner is essential for quantum sensors beyond the standard quantum limit. We demonstrate that Bayesian optimal control is capable of finding control pulses that drive trapped Rydberg atoms into highly entangled GHZ states. The control sequences that can be constructed in laboratory experiments result in preparation times that scale very favourably with the system size.

Preparation of ordered states in ultra-cold gases using Bayesian optimization

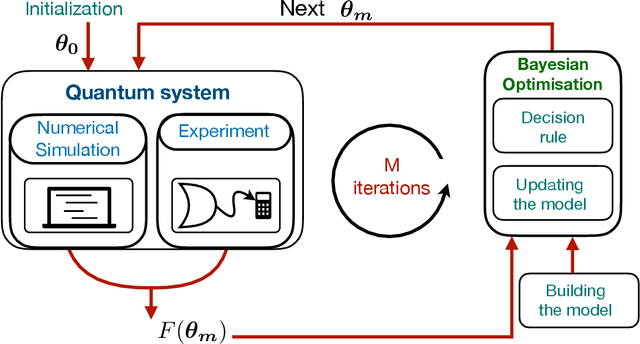
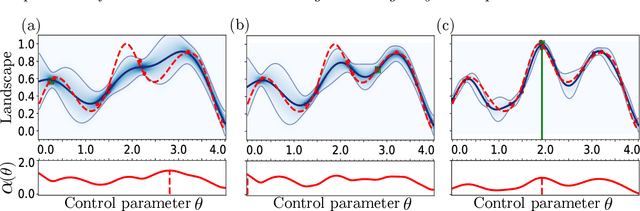
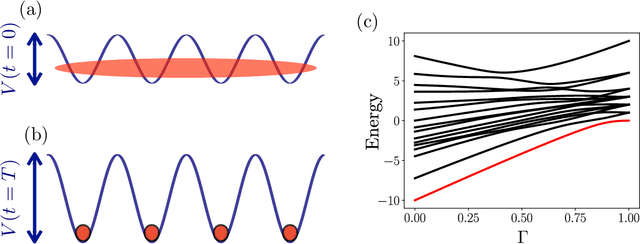
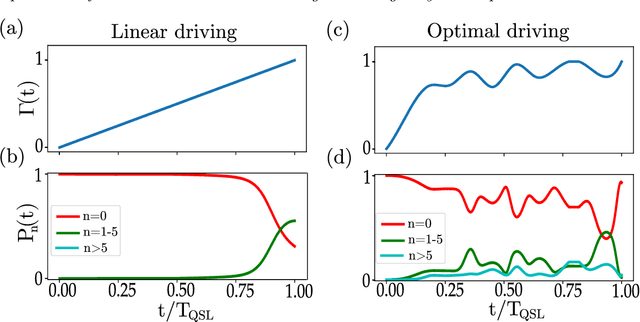
Ultra-cold atomic gases are unique in terms of the degree of controllability, both for internal and external degrees of freedom. This makes it possible to use them for the study of complex quantum many-body phenomena. However in many scenarios, the prerequisite condition of faithfully preparing a desired quantum state despite decoherence and system imperfections is not always adequately met. To path the way to a specific target state, we explore quantum optimal control framework based on Bayesian optimization. The probabilistic modeling and broad exploration aspects of Bayesian optimization is particularly suitable for quantum experiments where data acquisition can be expensive. Using numerical simulations for the superfluid to Mott-insulator transition for bosons in a lattice as well for the formation of Rydberg crystals as explicit examples, we demonstrate that Bayesian optimization is capable of finding better control solutions with regards to finite and noisy data compared to existing methods of optimal control.