Advancing Lazy-Grounding ASP Solving Techniques -- Restarts, Phase Saving, Heuristics, and More

Answer-Set Programming (ASP) is a powerful and expressive knowledge representation paradigm with a significant number of applications in logic-based AI. The traditional ground-and-solve approach, however, requires ASP programs to be grounded upfront and thus suffers from the so-called grounding bottleneck (i.e., ASP programs easily exhaust all available memory and thus become unsolvable). As a remedy, lazy-grounding ASP solvers have been developed, but many state-of-the-art techniques for grounded ASP solving have not been available to them yet. In this work we present, for the first time, adaptions to the lazy-grounding setting for many important techniques, like restarts, phase saving, domain-independent heuristics, and learned-clause deletion. Furthermore, we investigate their effects and in general observe a large improvement in solving capabilities and also uncover negative effects in certain cases, indicating the need for portfolio solving as known from other solvers. Under consideration for acceptance in TPLP.

Conflict Generalisation in ASP: Learning Correct and Effective Non-Ground Constraints

Generalising and re-using knowledge learned while solving one problem instance has been neglected by state-of-the-art answer set solvers. We suggest a new approach that generalises learned nogoods for re-use to speed-up the solving of future problem instances. Our solution combines well-known ASP solving techniques with deductive logic-based machine learning. Solving performance can be improved by adding learned non-ground constraints to the original program. We demonstrate the effects of our method by means of realistic examples, showing that our approach requires low computational cost to learn constraints that yield significant performance benefits in our test cases. These benefits can be seen with ground-and-solve systems as well as lazy-grounding systems. However, ground-and-solve systems suffer from additional grounding overheads, induced by the additional constraints in some cases. By means of conflict minimization, non-minimal learned constraints can be reduced. This can result in significant reductions of grounding and solving efforts, as our experiments show. (Under consideration for acceptance in TPLP.)

Exploiting Partial Knowledge in Declarative Domain-Specific Heuristics for ASP

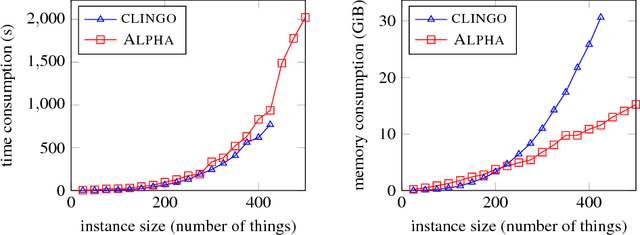
Domain-specific heuristics are an important technique for solving combinatorial problems efficiently. We propose a novel semantics for declarative specifications of domain-specific heuristics in Answer Set Programming (ASP). Decision procedures that are based on a partial solution are a frequent ingredient of existing domain-specific heuristics, e.g., for placing an item that has not been placed yet in bin packing. Therefore, in our novel semantics negation as failure and aggregates in heuristic conditions are evaluated on a partial solver state. State-of-the-art solvers do not allow such a declarative specification. Our implementation in the lazy-grounding ASP system Alpha supports heuristic directives under this semantics. By that, we also provide the first implementation for incorporating declaratively specified domain-specific heuristics in a lazy-grounding setting. Experiments confirm that the combination of ASP solving with lazy grounding and our novel heuristics can be a vital ingredient for solving industrial-size problems.

Degrees of Laziness in Grounding: Effects of Lazy-Grounding Strategies on ASP Solving

The traditional ground-and-solve approach to Answer Set Programming (ASP) suffers from the grounding bottleneck, which makes large-scale problem instances unsolvable. Lazy grounding is an alternative approach that interleaves grounding with solving and thus uses space more efficiently. The limited view on the search space in lazy grounding poses unique challenges, however, and can have adverse effects on solving performance. In this paper we present a novel characterization of degrees of laziness in grounding for ASP, i.e. of compromises between lazily grounding as little as possible and the traditional full grounding upfront. We investigate how these degrees of laziness compare to each other formally as well as, by means of an experimental analysis using a number of benchmarks, in terms of their effects on solving performance. Our contributions are the introduction of a range of novel lazy grounding strategies, a formal account on their relationships and their correctness, and an investigation of their effects on solving performance. Experiments show that our approach performs significantly better than state-of-the-art lazy grounding in many cases.