Riccardo Zucca
Scaling Properties of Human Brain Functional Networks
Feb 02, 2017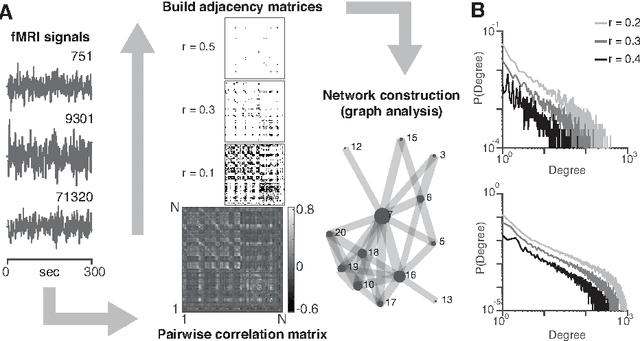
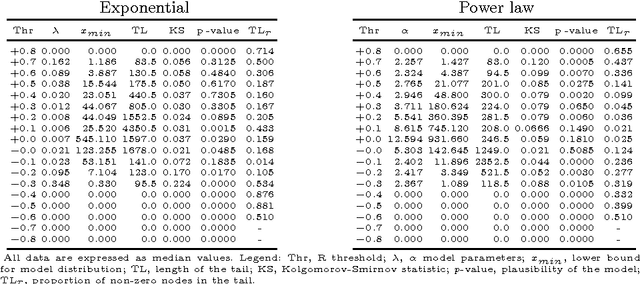

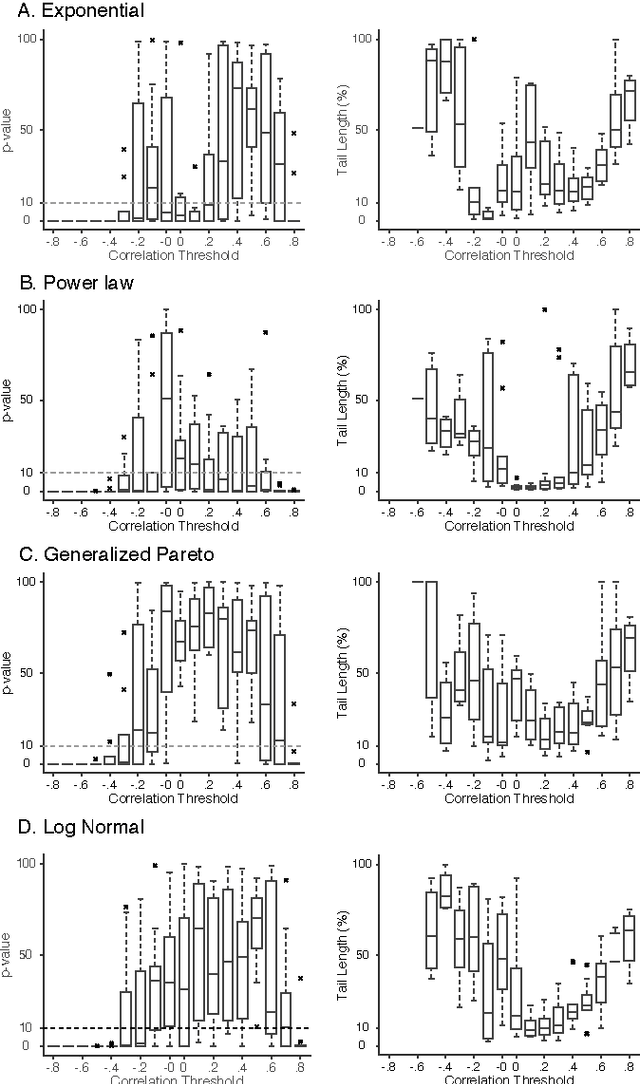
Abstract:We investigate scaling properties of human brain functional networks in the resting-state. Analyzing network degree distributions, we statistically test whether their tails scale as power-law or not. Initial studies, based on least-squares fitting, were shown to be inadequate for precise estimation of power-law distributions. Subsequently, methods based on maximum-likelihood estimators have been proposed and applied to address this question. Nevertheless, no clear consensus has emerged, mainly because results have shown substantial variability depending on the data-set used or its resolution. In this study, we work with high-resolution data (10K nodes) from the Human Connectome Project and take into account network weights. We test for the power-law, exponential, log-normal and generalized Pareto distributions. Our results show that the statistics generally do not support a power-law, but instead these degree distributions tend towards the thin-tail limit of the generalized Pareto model. This may have implications for the number of hubs in human brain functional networks.
* International Conference on Artificial Neural Networks - ICANN 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge