Regularized Pel-Recursive Motion Estimation Using Generalized Cross-Validation and Spatial Adaptation

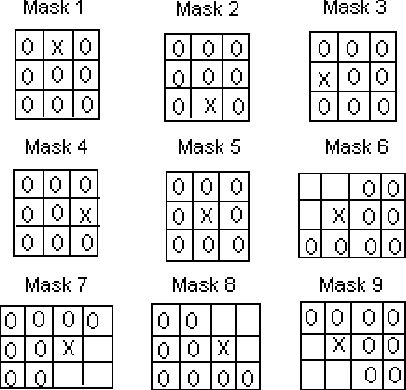
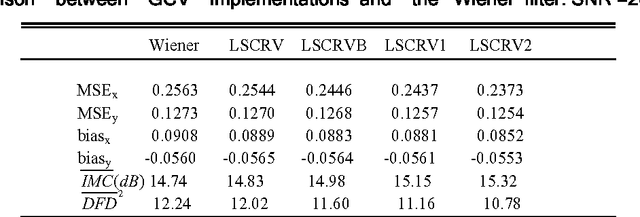
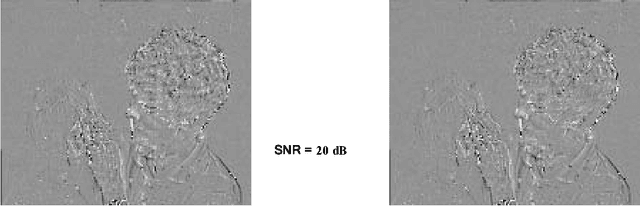
The computation of 2-D optical flow by means of regularized pel-recursive algorithms raises a host of issues, which include the treatment of outliers, motion discontinuities and occlusion among other problems. We propose a new approach which allows us to deal with these issues within a common framework. Our approach is based on the use of a technique called Generalized Cross-Validation to estimate the best regularization scheme for a given pixel. In our model, the regularization parameter is a matrix whose entries can account for diverse sources of error. The estimation of the motion vectors takes into consideration local properties of the image following a spatially adaptive approach where each moving pixel is supposed to have its own regularization matrix. Preliminary experiments indicate that this approach provides robust estimates of the optical flow.

Adaptive mixed norm optical flow estimation

The pel-recursive computation of 2-D optical flow has been extensively studied in computer vision to estimate motion from image sequences, but it still raises a wealth of issues, such as the treatment of outliers, motion discontinuities and occlusion. It relies on spatio-temporal brightness variations due to motion. Our proposed adaptive regularized approach deals with these issues within a common framework. It relies on the use of a data-driven technique called Mixed Norm (MN) to estimate the best motion vector for a given pixel. In our model, various types of noise can be handled, representing different sources of error. The motion vector estimation takes into consideration local image properties and it results from the minimization of a mixed norm functional with a regularization parameter depending on the kurtosis. This parameter determines the relative importance of the fourth norm and makes the functional convex. The main advantage of the developed procedure is that no knowledge of the noise distribution is necessary. Experiments indicate that this approach provides robust estimates of the optical flow.