Mixed-Stationary Gaussian Process for Flexible Non-Stationary Modeling of Spatial Outcomes

Gaussian processes (GPs) are commonplace in spatial statistics. Although many non-stationary models have been developed, there is arguably a lack of flexibility compared to equipping each location with its own parameters. However, the latter suffers from intractable computation and can lead to overfitting. Taking the instantaneous stationarity idea, we construct a non-stationary GP with the stationarity parameter individually set at each location. Then we utilize the non-parametric mixture model to reduce the effective number of unique parameters. Different from a simple mixture of independent GPs, the mixture in stationarity allows the components to be spatial correlated, leading to improved prediction efficiency. Theoretical properties are examined and a linearly scalable algorithm is provided. The application is shown through several simulated scenarios as well as the massive spatiotemporally correlated temperature data.

Functional Gaussian Process Model for Bayesian Nonparametric Analysis

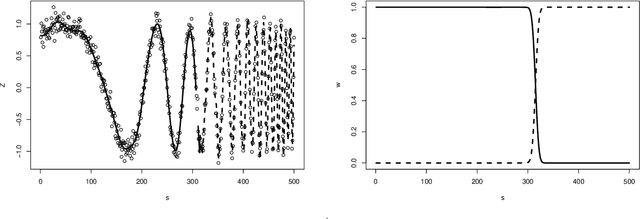
Gaussian process is a theoretically appealing model for nonparametric analysis, but its computational cumbersomeness hinders its use in large scale and the existing reduced-rank solutions are usually heuristic. In this work, we propose a novel construction of Gaussian process as a projection from fixed discrete frequencies to any continuous location. This leads to a valid stochastic process that has a theoretic support with the reduced rank in the spectral density, as well as a high-speed computing algorithm. Our method provides accurate estimates for the covariance parameters and concise form of predictive distribution for spatial prediction. For non-stationary data, we adopt the mixture framework with a customized spectral dependency structure. This enables clustering based on local stationarity, while maintains the joint Gaussianness. Our work is directly applicable in solving some of the challenges in the spatial data, such as large scale computation, anisotropic covariance, spatio-temporal modeling, etc. We illustrate the uses of the model via simulations and an application on a massive dataset.

Joint Hierarchical Gaussian Process Model with Application to Forecast in Medical Monitoring

A novel extrapolation method is proposed for longitudinal forecasting. A hierarchical Gaussian process model is used to combine nonlinear population change and individual memory of the past to make prediction. The prediction error is minimized through the hierarchical design. The method is further extended to joint modeling of continuous measurements and survival events. The baseline hazard, covariate and joint effects are conveniently modeled in this hierarchical structure. The estimation and inference are implemented in fully Bayesian framework using the objective and shrinkage priors. In simulation studies, this model shows robustness in latent estimation, correlation detection and high accuracy in forecasting. The model is illustrated with medical monitoring data from cystic fibrosis (CF) patients. Estimation and forecasts are obtained in the measurement of lung function and records of acute respiratory events. Keyword: Extrapolation, Joint Model, Longitudinal Model, Hierarchical Gaussian Process, Cystic Fibrosis, Medical Monitoring

BET: Bayesian Ensemble Trees for Clustering and Prediction in Heterogeneous Data

We propose a novel "tree-averaging" model that utilizes the ensemble of classification and regression trees (CART). Each constituent tree is estimated with a subset of similar data. We treat this grouping of subsets as Bayesian ensemble trees (BET) and model them as an infinite mixture Dirichlet process. We show that BET adapts to data heterogeneity and accurately estimates each component. Compared with the bootstrap-aggregating approach, BET shows improved prediction performance with fewer trees. We develop an efficient estimating procedure with improved sampling strategies in both CART and mixture models. We demonstrate these advantages of BET with simulations, classification of breast cancer and regression of lung function measurement of cystic fibrosis patients. Keywords: Bayesian CART; Dirichlet Process; Ensemble Approach; Heterogeneity; Mixture of Trees.