Functional Gaussian Process Model for Bayesian Nonparametric Analysis
Paper and Code
Nov 24, 2015

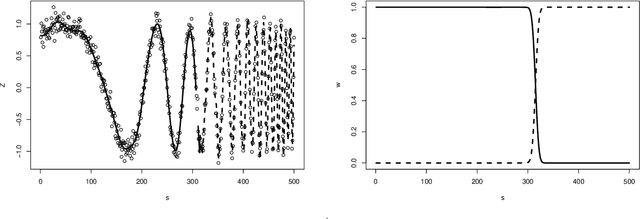
Gaussian process is a theoretically appealing model for nonparametric analysis, but its computational cumbersomeness hinders its use in large scale and the existing reduced-rank solutions are usually heuristic. In this work, we propose a novel construction of Gaussian process as a projection from fixed discrete frequencies to any continuous location. This leads to a valid stochastic process that has a theoretic support with the reduced rank in the spectral density, as well as a high-speed computing algorithm. Our method provides accurate estimates for the covariance parameters and concise form of predictive distribution for spatial prediction. For non-stationary data, we adopt the mixture framework with a customized spectral dependency structure. This enables clustering based on local stationarity, while maintains the joint Gaussianness. Our work is directly applicable in solving some of the challenges in the spatial data, such as large scale computation, anisotropic covariance, spatio-temporal modeling, etc. We illustrate the uses of the model via simulations and an application on a massive dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge