Reza Bosagh Zadeh
Dimension Independent Similarity Computation
May 23, 2013
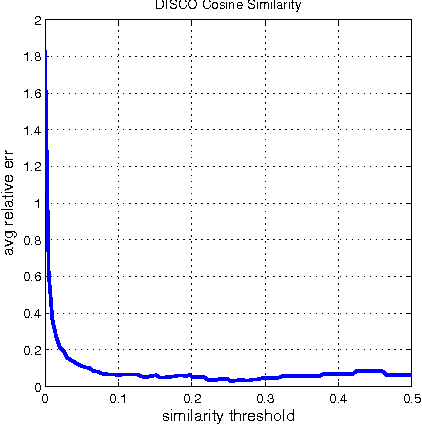
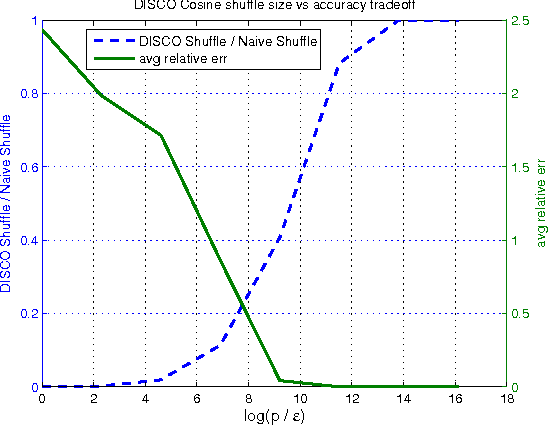
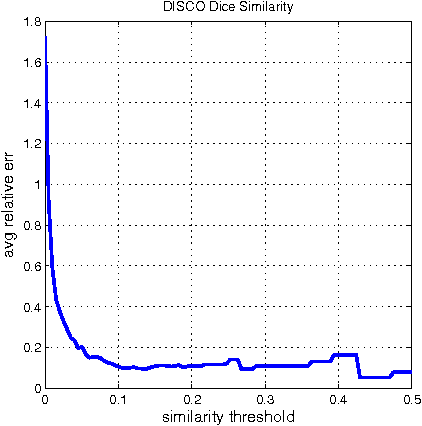
Abstract:We present a suite of algorithms for Dimension Independent Similarity Computation (DISCO) to compute all pairwise similarities between very high dimensional sparse vectors. All of our results are provably independent of dimension, meaning apart from the initial cost of trivially reading in the data, all subsequent operations are independent of the dimension, thus the dimension can be very large. We study Cosine, Dice, Overlap, and the Jaccard similarity measures. For Jaccard similiarity we include an improved version of MinHash. Our results are geared toward the MapReduce framework. We empirically validate our theorems at large scale using data from the social networking site Twitter. At time of writing, our algorithms are live in production at twitter.com.
A Uniqueness Theorem for Clustering
May 09, 2012
Abstract:Despite the widespread use of Clustering, there is distressingly little general theory of clustering available. Questions like "What distinguishes a clustering of data from other data partitioning?", "Are there any principles governing all clustering paradigms?", "How should a user choose an appropriate clustering algorithm for a particular task?", etc. are almost completely unanswered by the existing body of clustering literature. We consider an axiomatic approach to the theory of Clustering. We adopt the framework of Kleinberg, [Kle03]. By relaxing one of Kleinberg's clustering axioms, we sidestep his impossibility result and arrive at a consistent set of axioms. We suggest to extend these axioms, aiming to provide an axiomatic taxonomy of clustering paradigms. Such a taxonomy should provide users some guidance concerning the choice of the appropriate clustering paradigm for a given task. The main result of this paper is a set of abstract properties that characterize the Single-Linkage clustering function. This characterization result provides new insight into the properties of desired data groupings that make Single-Linkage the appropriate choice. We conclude by considering a taxonomy of clustering functions based on abstract properties that each satisfies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge