Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Renzo Cavalieri
Locally Linear Attributes of ReLU Neural Networks
Nov 30, 2020Figures and Tables: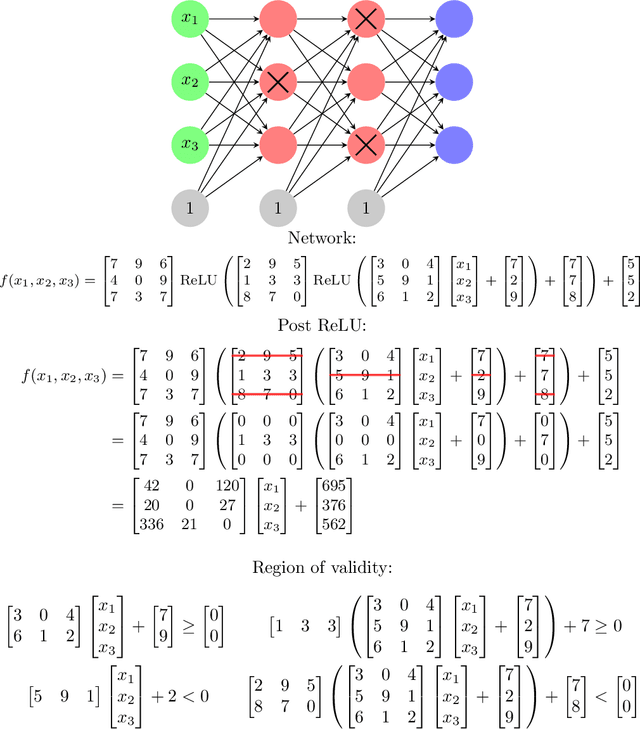
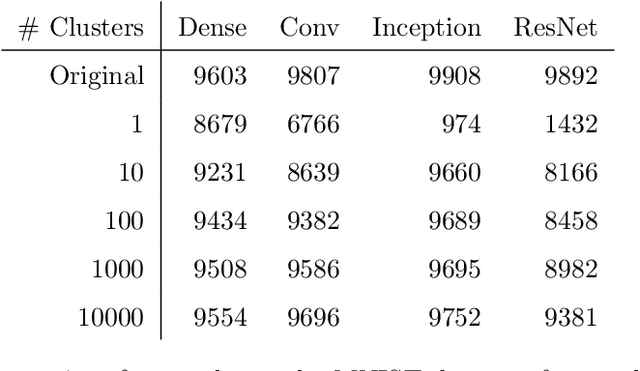
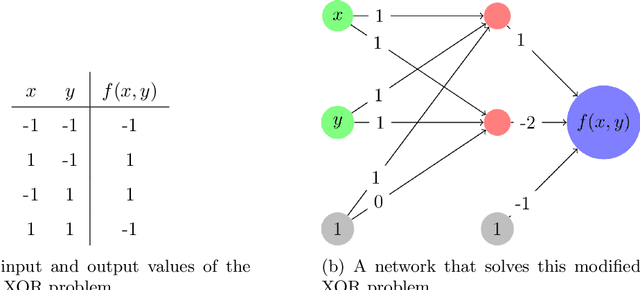
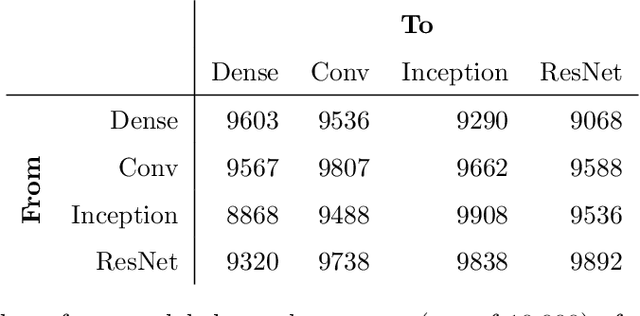




Abstract:A ReLU neural network determines/is a continuous piecewise linear map from an input space to an output space. The weights in the neural network determine a decomposition of the input space into convex polytopes and on each of these polytopes the network can be described by a single affine mapping. The structure of the decomposition, together with the affine map attached to each polytope, can be analyzed to investigate the behavior of the associated neural network.
* 18 pages, 12 figures, 2 tables, submitted to SIMODS
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge