Reka A. Kovacs
Binary Matrix Factorisation and Completion via Integer Programming
Jun 25, 2021

Abstract:Binary matrix factorisation is an essential tool for identifying discrete patterns in binary data. In this paper we consider the rank-k binary matrix factorisation problem (k-BMF) under Boolean arithmetic: we are given an n x m binary matrix X with possibly missing entries and need to find two binary matrices A and B of dimension n x k and k x m respectively, which minimise the distance between X and the Boolean product of A and B in the squared Frobenius distance. We present a compact and two exponential size integer programs (IPs) for k-BMF and show that the compact IP has a weak LP relaxation, while the exponential size LPs have a stronger equivalent LP relaxation. We introduce a new objective function, which differs from the traditional squared Frobenius objective in attributing a weight to zero entries of the input matrix that is proportional to the number of times the zero is erroneously covered in a rank-k factorisation. For one of the exponential size IPs we describe a computational approach based on column generation. Experimental results on synthetic and real word datasets suggest that our integer programming approach is competitive against available methods for k-BMF and provides accurate low-error factorisations.
Binary Matrix Factorisation via Column Generation
Nov 09, 2020
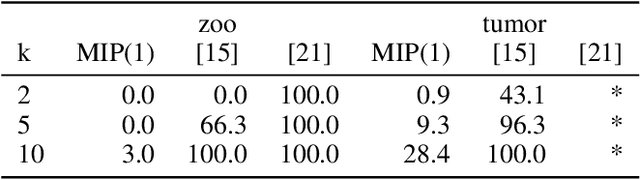

Abstract:Identifying discrete patterns in binary data is an important dimensionality reduction tool in machine learning and data mining. In this paper, we consider the problem of low-rank binary matrix factorisation (BMF) under Boolean arithmetic. Due to the NP-hardness of this problem, most previous attempts rely on heuristic techniques. We formulate the problem as a mixed integer linear program and use a large scale optimisation technique of column generation to solve it without the need of heuristic pattern mining. Our approach focuses on accuracy and on the provision of optimality guarantees. Experimental results on real world datasets demonstrate that our proposed method is effective at producing highly accurate factorisations and improves on the previously available best known results for 16 out of 24 problem instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge