Binary Matrix Factorisation and Completion via Integer Programming
Paper and Code
Jun 25, 2021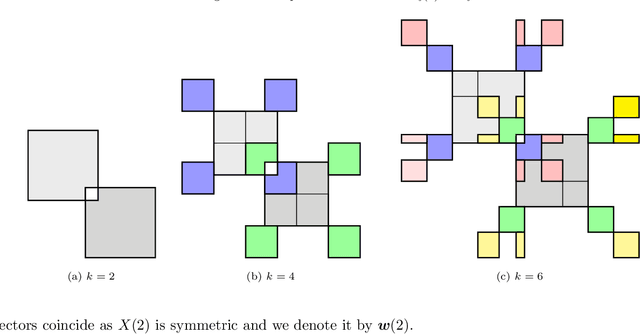

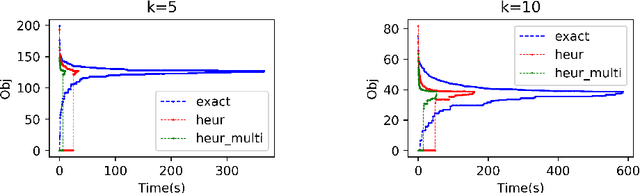
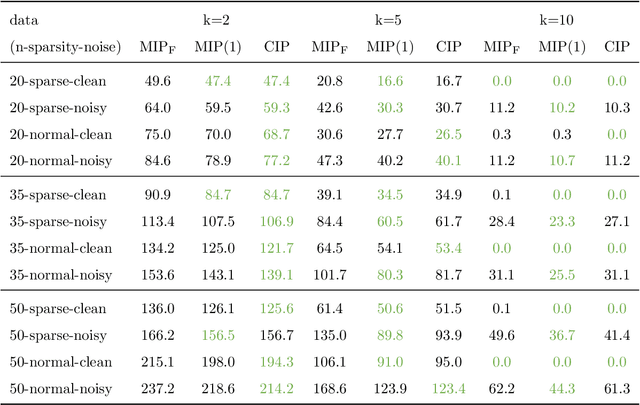
Binary matrix factorisation is an essential tool for identifying discrete patterns in binary data. In this paper we consider the rank-k binary matrix factorisation problem (k-BMF) under Boolean arithmetic: we are given an n x m binary matrix X with possibly missing entries and need to find two binary matrices A and B of dimension n x k and k x m respectively, which minimise the distance between X and the Boolean product of A and B in the squared Frobenius distance. We present a compact and two exponential size integer programs (IPs) for k-BMF and show that the compact IP has a weak LP relaxation, while the exponential size LPs have a stronger equivalent LP relaxation. We introduce a new objective function, which differs from the traditional squared Frobenius objective in attributing a weight to zero entries of the input matrix that is proportional to the number of times the zero is erroneously covered in a rank-k factorisation. For one of the exponential size IPs we describe a computational approach based on column generation. Experimental results on synthetic and real word datasets suggest that our integer programming approach is competitive against available methods for k-BMF and provides accurate low-error factorisations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge