SymptomAI: Towards a Conversational AI Agent for Everyday Symptom Assessment

Language models excel at diagnostic assessments on currated medical case-studies and vignettes, performing on par with, or better than, clinical professionals. However, existing studies focus on complex scenarios with rich context making it difficult to draw conclusions about how these systems perform for patients reporting symptoms in everyday life. We deployed SymptomAI, a set of conversational AI agents for end-to-end patient interviewing and differential diagnosis (DDx), via the Fitbit app in a study that randomized participants (N=13,917) to interact with five AI agents. This corpus captures diverse communication and a realistic distribution of illnesses from a real world population. A subset of 1,228 participants reported a clinician-provided diagnosis, and 517 of these were further evaluated by a panel of clinicians during over 250 hours of annotation. SymptomAI DDx were significantly more accurate (OR = 2.47, p < 0.001) than those from independent clinicians given the same dialogue in a blinded randomized comparison. Moreover, agentic strategies which conduct a dedicated symptom interview that elicit additional symptom information before providing a diagnosis, perform substantially better than baseline, user-guided conversations (p < 0.001). An auxiliary analysis on 1,509 conversations from a general US population panel validated that these results generalize beyond wearable device users. We used SymptomAI diagnoses as labels for all 13,917 participants to analyze over 500,000 days of wearable metrics across nearly 400 unique conditions. We identified strong associations between acute infections and physiological shifts (e.g., OR > 7 for influenza). While limited by self-reported ground truth, these results demonstrate the benefits of a dedicated and complete symptom interview compared to a user-guided symptom discussion, which is the default of most consumer LLMs.

End-to-End Reaction Field Energy Modeling via Deep Learning based Voxel-to-voxel Transform

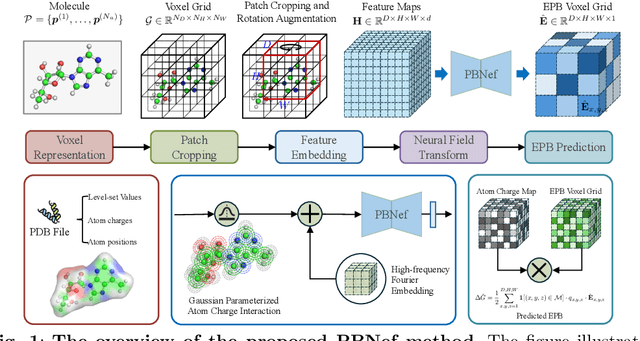
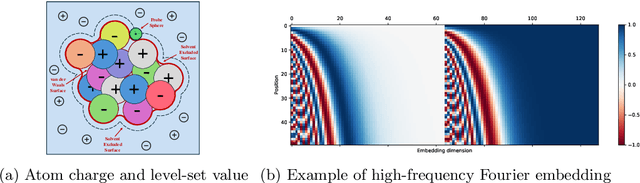
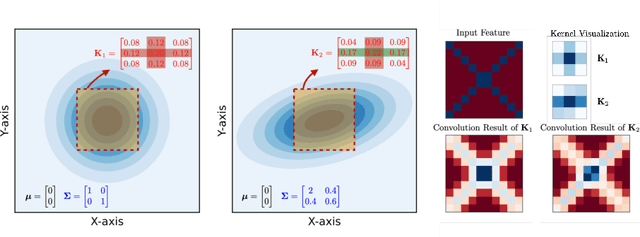
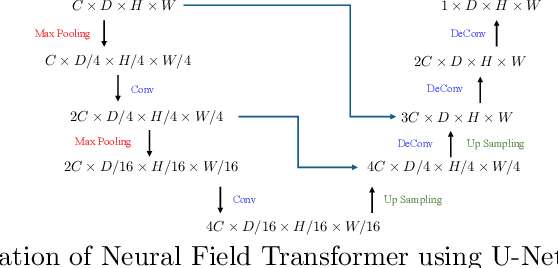
In computational biochemistry and biophysics, understanding the role of electrostatic interactions is crucial for elucidating the structure, dynamics, and function of biomolecules. The Poisson-Boltzmann (PB) equation is a foundational tool for modeling these interactions by describing the electrostatic potential in and around charged molecules. However, solving the PB equation presents significant computational challenges due to the complexity of biomolecular surfaces and the need to account for mobile ions. While traditional numerical methods for solving the PB equation are accurate, they are computationally expensive and scale poorly with increasing system size. To address these challenges, we introduce PBNeF, a novel machine learning approach inspired by recent advancements in neural network-based partial differential equation solvers. Our method formulates the input and boundary electrostatic conditions of the PB equation into a learnable voxel representation, enabling the use of a neural field transformer to predict the PB solution and, subsequently, the reaction field potential energy. Extensive experiments demonstrate that PBNeF achieves over a 100-fold speedup compared to traditional PB solvers, while maintaining accuracy comparable to the Generalized Born (GB) model.