Raquel Vidaurre
Fully Convolutional Graph Neural Networks for Parametric Virtual Try-On
Sep 09, 2020



Abstract:We present a learning-based approach for virtual try-on applications based on a fully convolutional graph neural network. In contrast to existing data-driven models, which are trained for a specific garment or mesh topology, our fully convolutional model can cope with a large family of garments, represented as parametric predefined 2D panels with arbitrary mesh topology, including long dresses, shirts, and tight tops. Under the hood, our novel geometric deep learning approach learns to drape 3D garments by decoupling the three different sources of deformations that condition the fit of clothing: garment type, target body shape, and material. Specifically, we first learn a regressor that predicts the 3D drape of the input parametric garment when worn by a mean body shape. Then, after a mesh topology optimization step where we generate a sufficient level of detail for the input garment type, we further deform the mesh to reproduce deformations caused by the target body shape. Finally, we predict fine-scale details such as wrinkles that depend mostly on the garment material. We qualitatively and quantitatively demonstrate that our fully convolutional approach outperforms existing methods in terms of generalization capabilities and memory requirements, and therefore it opens the door to more general learning-based models for virtual try-on applications.
BRDF Estimation of Complex Materials with Nested Learning
Nov 22, 2018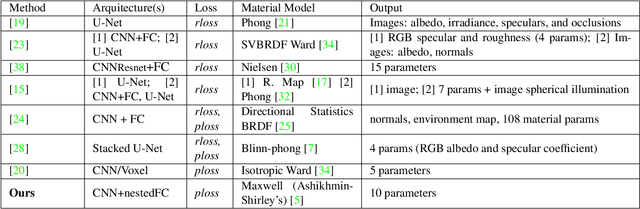



Abstract:The estimation of the optical properties of a material from RGB-images is an important but extremely ill-posed problem in Computer Graphics. While recent works have successfully approached this problem even from just a single photograph, significant simplifications of the material model are assumed, limiting the usability of such methods. The detection of complex material properties such as anisotropy or Fresnel effect remains an unsolved challenge. We propose a novel method that predicts the model parameters of an artist-friendly, physically-based BRDF, from only two low-resolution shots of the material. Thanks to a novel combination of deep neural networks in a nested architecture, we are able to handle the ambiguities given by the non-orthogonality and non-convexity of the parameter space. To train the network, we generate a novel dataset of physically-based synthetic images. We prove that our model can recover new properties like anisotropy, index of refraction and a second reflectance color, for materials that have tinted specular reflections or whose albedo changes at glancing angles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge