Predicting Tropical Cyclone Track Forecast Errors using a Probabilistic Neural Network

A new method for estimating tropical cyclone track uncertainty is presented and tested. This method uses a neural network to predict a bivariate normal distribution, which serves as an estimate for track uncertainty. We train the network and make predictions on forecasts from the National Hurricane Center (NHC), which currently uses static error distributions based on forecasts from the past five years for most applications. The neural network-based method produces uncertainty estimates that are dynamic and probabilistic. Further, the neural network-based method allows for probabilistic statements about tropical cyclone trajectories, including landfall probability, which we highlight. We show that our predictions are well calibrated using multiple metrics, that our method produces better uncertainty estimates than current NHC approaches, and that our method achieves similar performance to the Global Ensemble Forecast System. Once trained, the computational cost of predictions using this method is negligible, making it a strong candidate to improve the NHC's operational estimations of tropical cyclone track uncertainty.

Controlled abstention neural networks for identifying skillful predictions for classification problems

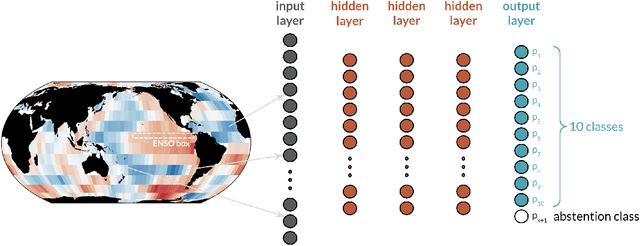
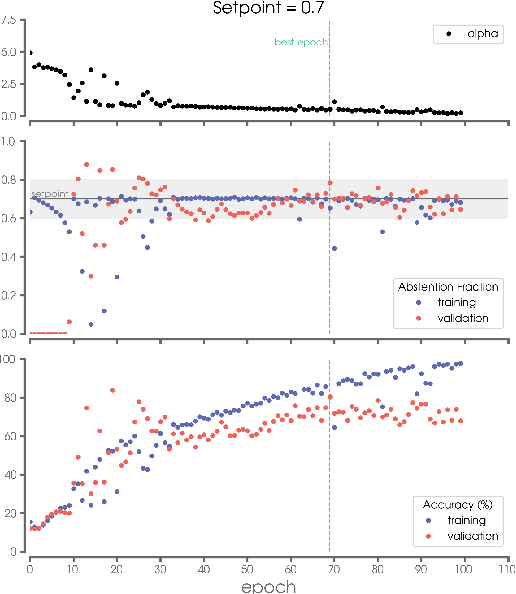
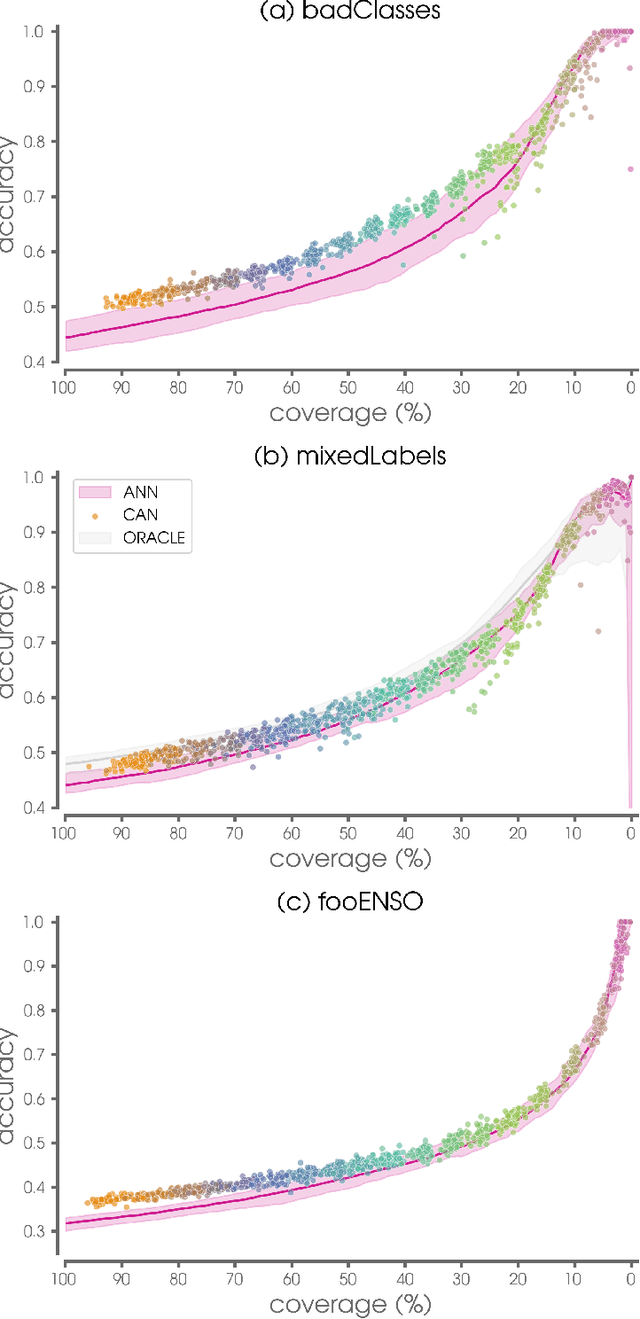
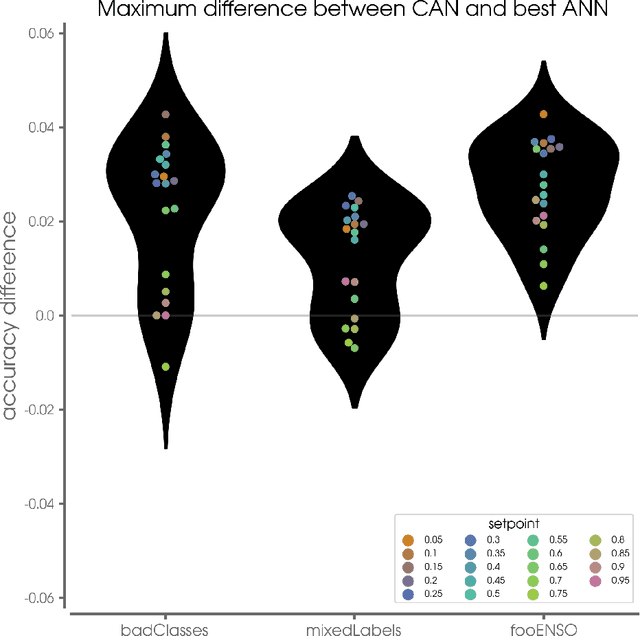
The earth system is exceedingly complex and often chaotic in nature, making prediction incredibly challenging: we cannot expect to make perfect predictions all of the time. Instead, we look for specific states of the system that lead to more predictable behavior than others, often termed "forecasts of opportunity." When these opportunities are not present, scientists need prediction systems that are capable of saying "I don't know." We introduce a novel loss function, termed the "NotWrong loss", that allows neural networks to identify forecasts of opportunity for classification problems. The NotWrong loss introduces an abstention class that allows the network to identify the more confident samples and abstain (say "I don't know") on the less confident samples. The abstention loss is designed to abstain on a user-defined fraction of the samples via a PID controller. Unlike many machine learning methods used to reject samples post-training, the NotWrong loss is applied during training to preferentially learn from the more confident samples. We show that the NotWrong loss outperforms other existing loss functions for multiple climate use cases. The implementation of the proposed loss function is straightforward in most network architectures designed for classification as it only requires the addition of an abstention class to the output layer and modification of the loss function.

Controlled abstention neural networks for identifying skillful predictions for regression problems

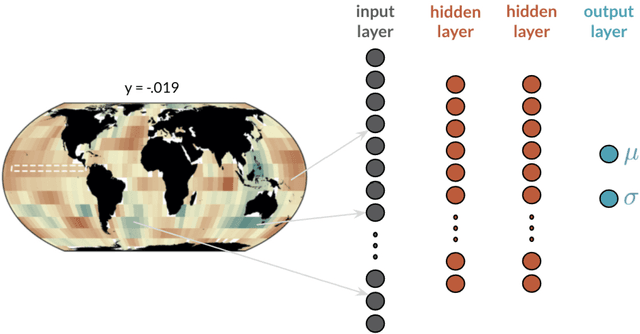
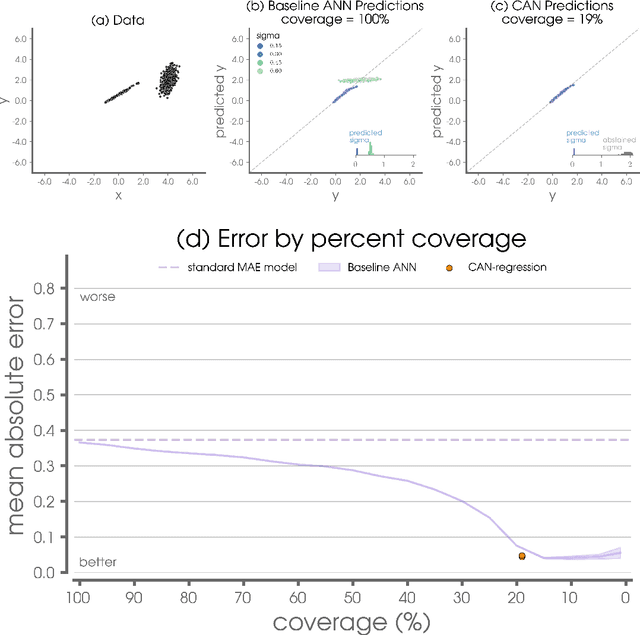
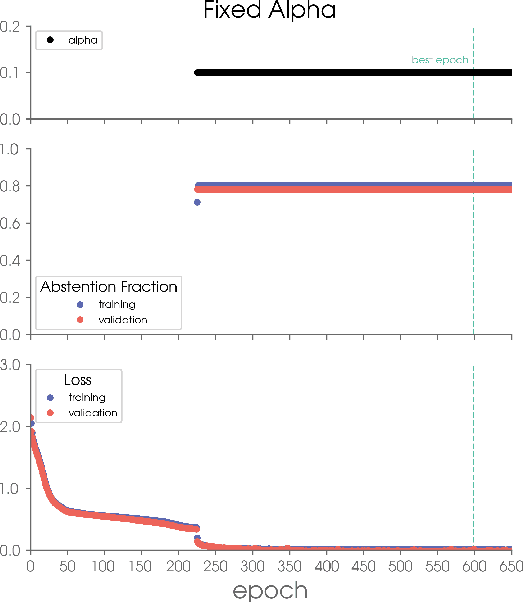
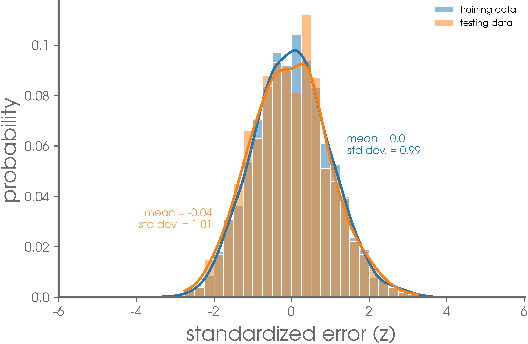
The earth system is exceedingly complex and often chaotic in nature, making prediction incredibly challenging: we cannot expect to make perfect predictions all of the time. Instead, we look for specific states of the system that lead to more predictable behavior than others, often termed "forecasts of opportunity". When these opportunities are not present, scientists need prediction systems that are capable of saying "I don't know." We introduce a novel loss function, termed "abstention loss", that allows neural networks to identify forecasts of opportunity for regression problems. The abstention loss works by incorporating uncertainty in the network's prediction to identify the more confident samples and abstain (say "I don't know") on the less confident samples. The abstention loss is designed to determine the optimal abstention fraction, or abstain on a user-defined fraction via a PID controller. Unlike many methods for attaching uncertainty to neural network predictions post-training, the abstention loss is applied during training to preferentially learn from the more confident samples. The abstention loss is built upon a standard computer science method. While the standard approach is itself a simple yet powerful tool for incorporating uncertainty in regression problems, we demonstrate that the abstention loss outperforms this more standard method for the synthetic climate use cases explored here. The implementation of proposed loss function is straightforward in most network architectures designed for regression, as it only requires modification of the output layer and loss function.