On Continuity of Robust and Accurate Classifiers

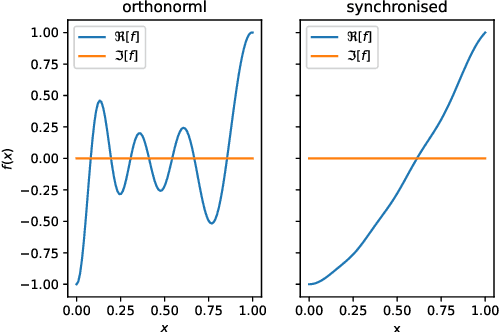
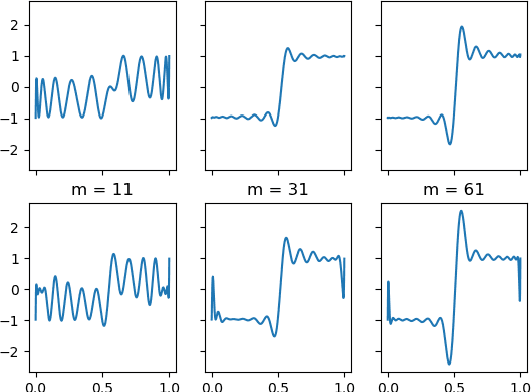
The reliability of a learning model is key to the successful deployment of machine learning in various applications. Creating a robust model, particularly one unaffected by adversarial attacks, requires a comprehensive understanding of the adversarial examples phenomenon. However, it is difficult to describe the phenomenon due to the complicated nature of the problems in machine learning. It has been shown that adversarial training can improve the robustness of the hypothesis. However, this improvement comes at the cost of decreased performance on natural samples. Hence, it has been suggested that robustness and accuracy of a hypothesis are at odds with each other. In this paper, we put forth the alternative proposal that it is the continuity of a hypothesis that is incompatible with its robustness and accuracy. In other words, a continuous function cannot effectively learn the optimal robust hypothesis. To this end, we will introduce a framework for a rigorous study of harmonic and holomorphic hypothesis in learning theory terms and provide empirical evidence that continuous hypotheses does not perform as well as discontinuous hypotheses in some common machine learning tasks. From a practical point of view, our results suggests that a robust and accurate learning rule would train different continuous hypotheses for different regions of the domain. From a theoretical perspective, our analysis explains the adversarial examples phenomenon as a conflict between the continuity of a sequence of functions and its uniform convergence to a discontinuous function.

An Analytic Framework for Robust Training of Artificial Neural Networks

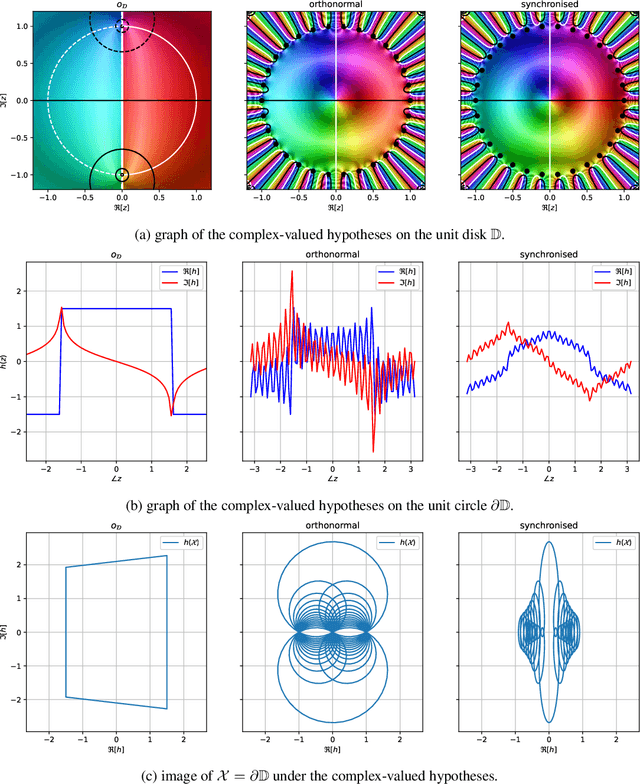
The reliability of a learning model is key to the successful deployment of machine learning in various industries. Creating a robust model, particularly one unaffected by adversarial attacks, requires a comprehensive understanding of the adversarial examples phenomenon. However, it is difficult to describe the phenomenon due to the complicated nature of the problems in machine learning. Consequently, many studies investigate the phenomenon by proposing a simplified model of how adversarial examples occur and validate it by predicting some aspect of the phenomenon. While these studies cover many different characteristics of the adversarial examples, they have not reached a holistic approach to the geometric and analytic modeling of the phenomenon. This paper propose a formal framework to study the phenomenon in learning theory and make use of complex analysis and holomorphicity to offer a robust learning rule for artificial neural networks. With the help of complex analysis, we can effortlessly move between geometric and analytic perspectives of the phenomenon and offer further insights on the phenomenon by revealing its connection with harmonic functions. Using our model, we can explain some of the most intriguing characteristics of adversarial examples, including transferability of adversarial examples, and pave the way for novel approaches to mitigate the effects of the phenomenon.

Towards Explaining Adversarial Examples Phenomenon in Artificial Neural Networks

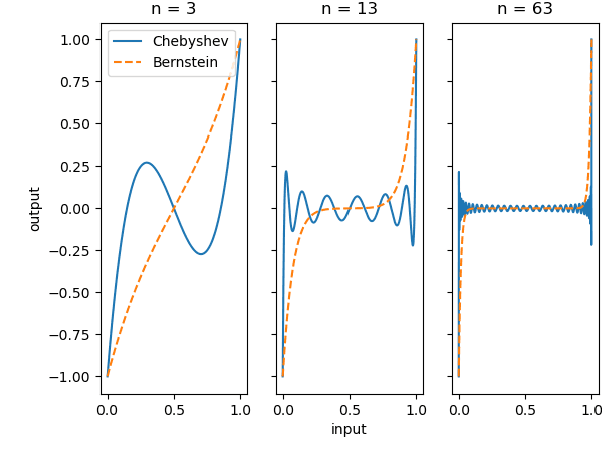
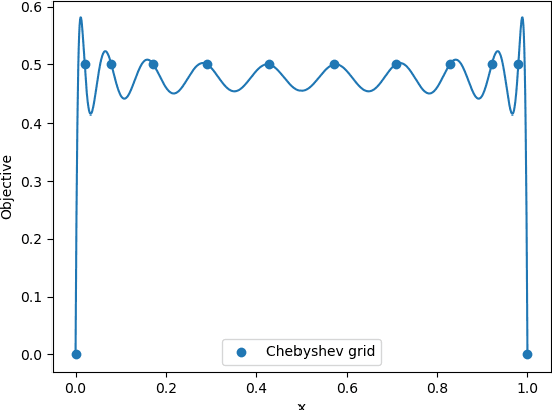
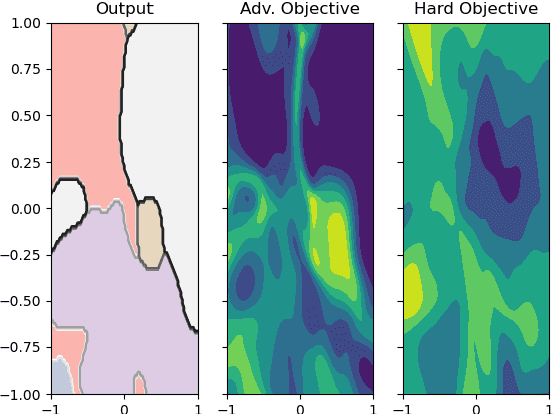
In this paper, we study the adversarial examples existence and adversarial training from the standpoint of convergence and provide evidence that pointwise convergence in ANNs can explain these observations. The main contribution of our proposal is that it relates the objective of the evasion attacks and adversarial training with concepts already defined in learning theory. Also, we extend and unify some of the other proposals in the literature and provide alternative explanations on the observations made in those proposals. Through different experiments, we demonstrate that the framework is valuable in the study of the phenomenon and is applicable to real-world problems.