Raju Ram
Scalable Hyperparameter Optimization with Lazy Gaussian Processes
Jan 16, 2020

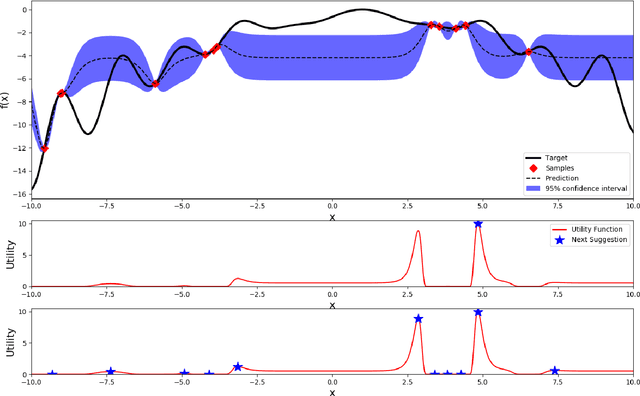
Abstract:Most machine learning methods require careful selection of hyper-parameters in order to train a high performing model with good generalization abilities. Hence, several automatic selection algorithms have been introduced to overcome tedious manual (try and error) tuning of these parameters. Due to its very high sample efficiency, Bayesian Optimization over a Gaussian Processes modeling of the parameter space has become the method of choice. Unfortunately, this approach suffers from a cubic compute complexity due to underlying Cholesky factorization, which makes it very hard to be scaled beyond a small number of sampling steps. In this paper, we present a novel, highly accurate approximation of the underlying Gaussian Process. Reducing its computational complexity from cubic to quadratic allows an efficient strong scaling of Bayesian Optimization while outperforming the previous approach regarding optimization accuracy. The first experiments show speedups of a factor of 162 in single node and further speed up by a factor of 5 in a parallel environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge