A Game-Theoretic Model Motivated by the DARPA Network Challenge

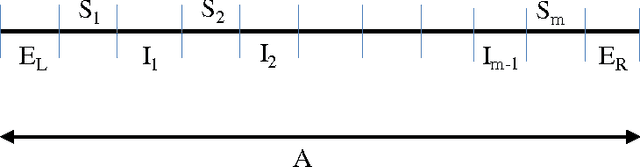
In this paper we propose a game-theoretic model to analyze events similar to the 2009 \emph{DARPA Network Challenge}, which was organized by the Defense Advanced Research Projects Agency (DARPA) for exploring the roles that the Internet and social networks play in incentivizing wide-area collaborations. The challenge was to form a group that would be the first to find the locations of ten moored weather balloons across the United States. We consider a model in which $N$ people (who can form groups) are located in some topology with a fixed coverage volume around each person's geographical location. We consider various topologies where the players can be located such as the Euclidean $d$-dimension space and the vertices of a graph. A balloon is placed in the space and a group wins if it is the first one to report the location of the balloon. A larger team has a higher probability of finding the balloon, but we assume that the prize money is divided equally among the team members. Hence there is a competing tension to keep teams as small as possible. \emph{Risk aversion} is the reluctance of a person to accept a bargain with an uncertain payoff rather than another bargain with a more certain, but possibly lower, expected payoff. In our model we consider the \emph{isoelastic} utility function derived from the Arrow-Pratt measure of relative risk aversion. The main aim is to analyze the structures of the groups in Nash equilibria for our model. For the $d$-dimensional Euclidean space ($d\geq 1$) and the class of bounded degree regular graphs we show that in any Nash Equilibrium the \emph{richest} group (having maximum expected utility per person) covers a constant fraction of the total volume.

Parameterized Complexity of Problems in Coalitional Resource Games

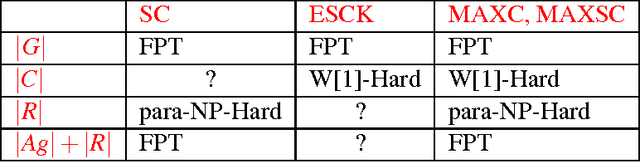
Coalition formation is a key topic in multi-agent systems. Coalitions enable agents to achieve goals that they may not have been able to achieve on their own. Previous work has shown problems in coalitional games to be computationally hard. Wooldridge and Dunne (Artificial Intelligence 2006) studied the classical computational complexity of several natural decision problems in Coalitional Resource Games (CRG) - games in which each agent is endowed with a set of resources and coalitions can bring about a set of goals if they are collectively endowed with the necessary amount of resources. The input of coalitional resource games bundles together several elements, e.g., the agent set Ag, the goal set G, the resource set R, etc. Shrot, Aumann and Kraus (AAMAS 2009) examine coalition formation problems in the CRG model using the theory of Parameterized Complexity. Their refined analysis shows that not all parts of input act equal - some instances of the problem are indeed tractable while others still remain intractable. We answer an important question left open by Shrot, Aumann and Kraus by showing that the SC Problem (checking whether a Coalition is Successful) is W[1]-hard when parameterized by the size of the coalition. Then via a single theme of reduction from SC, we are able to show that various problems related to resources, resource bounds and resource conflicts introduced by Wooldridge et al are 1. W[1]-hard or co-W[1]-hard when parameterized by the size of the coalition. 2. para-NP-hard or co-para-NP-hard when parameterized by |R|. 3. FPT when parameterized by either |G| or |Ag|+|R|.