Răzvan V. Florian
SuperCoder: Program Learning Under Noisy Conditions From Superposition of States
Dec 07, 2020
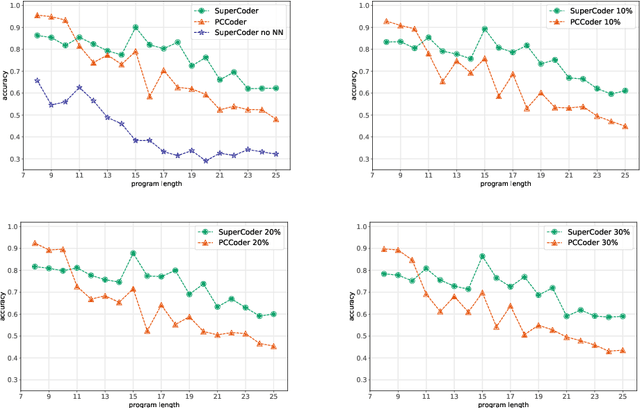
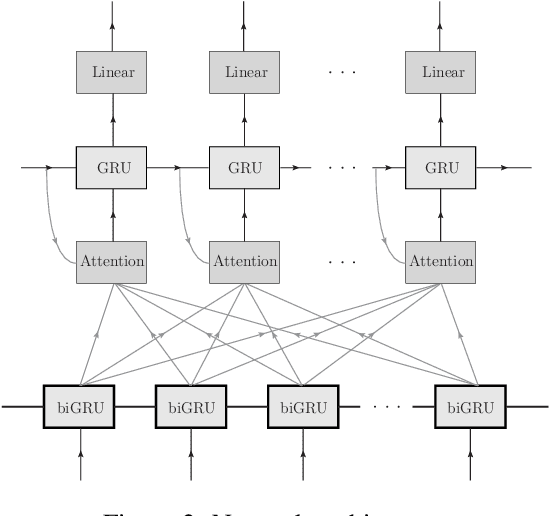
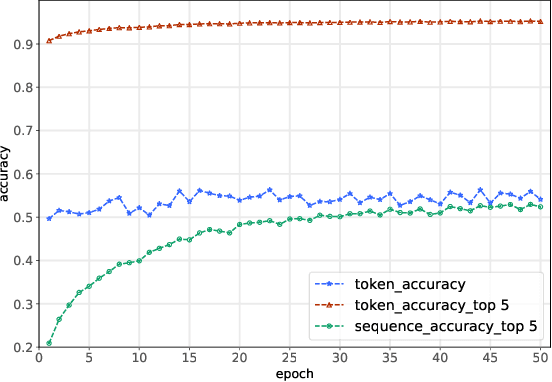
Abstract:We propose a new method of program learning in a Domain Specific Language (DSL) which is based on gradient descent with no direct search. The first component of our method is a probabilistic representation of the DSL variables. At each timestep in the program sequence, different DSL functions are applied on the DSL variables with a certain probability, leading to different possible outcomes. Rather than handling all these outputs separately, whose number grows exponentially with each timestep, we collect them into a superposition of variables which captures the information in a single, but fuzzy, state. This state is to be contrasted at the final timestep with the ground-truth output, through a loss function. The second component of our method is an attention-based recurrent neural network, which provides an appropriate initialization point for the gradient descent that optimizes the probabilistic representation. The method we have developed surpasses the state-of-the-art for synthesising long programs and is able to learn programs under noise.
A new class of metrics for spike trains
Jan 17, 2014Abstract:The distance between a pair of spike trains, quantifying the differences between them, can be measured using various metrics. Here we introduce a new class of spike train metrics, inspired by the Pompeiu-Hausdorff distance, and compare them with existing metrics. Some of our new metrics (the modulus-metric and the max-metric) have characteristics that are qualitatively different than those of classical metrics like the van Rossum distance or the Victor & Purpura distance. The modulus-metric and the max-metric are particularly suitable for measuring distances between spike trains where information is encoded in bursts, but the number and the timing of spikes inside a burst does not carry information. The modulus-metric does not depend on any parameters and can be computed using a fast algorithm, in a time that depends linearly on the number of spikes in the two spike trains. We also introduce localized versions of the new metrics, which could have the biologically-relevant interpretation of measuring the differences between spike trains as they are perceived at a particular moment in time by a neuron receiving these spike trains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge