Robust subspace clustering by Cauchy loss function

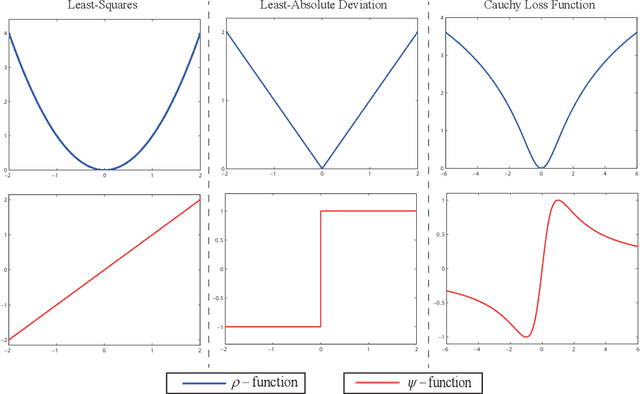
Subspace clustering is a problem of exploring the low-dimensional subspaces of high-dimensional data. State-of-the-arts approaches are designed by following the model of spectral clustering based method. These methods pay much attention to learn the representation matrix to construct a suitable similarity matrix and overlook the influence of the noise term on subspace clustering. However, the real data are always contaminated by the noise and the noise usually has a complicated statistical distribution. To alleviate this problem, we in this paper propose a subspace clustering method based on Cauchy loss function (CLF). Particularly, it uses CLF to penalize the noise term for suppressing the large noise mixed in the real data. This is due to that the CLF's influence function has a upper bound which can alleviate the influence of a single sample, especially the sample with a large noise, on estimating the residuals. Furthermore, we theoretically prove the grouping effect of our proposed method, which means that highly correlated data can be grouped together. Finally, experimental results on five real datasets reveal that our proposed method outperforms several representative clustering methods.

SCE: A manifold regularized set-covering method for data partitioning

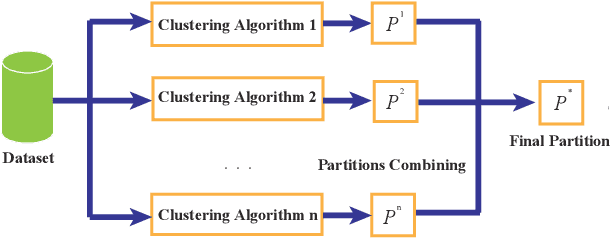
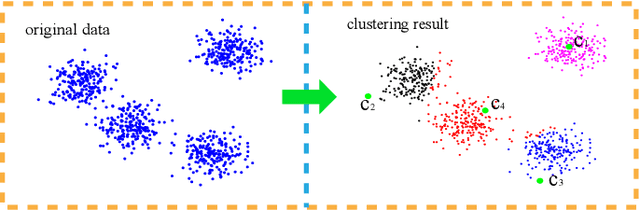
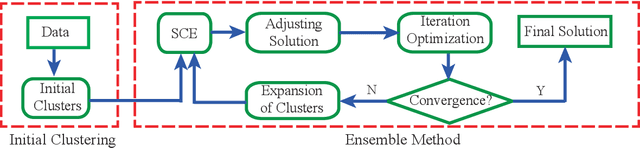
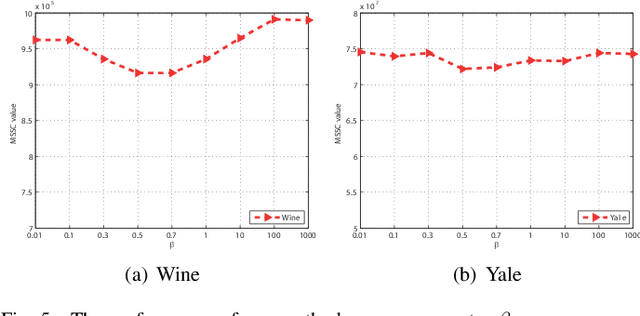
Cluster analysis plays a very important role in data analysis. In these years, cluster ensemble, as a cluster analysis tool, has drawn much attention for its robustness, stability, and accuracy. Many efforts have been done to combine different initial clustering results into a single clustering solution with better performance. However, they neglect the structure information of the raw data in performing the cluster ensemble. In this paper, we propose a Structural Cluster Ensemble (SCE) algorithm for data partitioning formulated as a set-covering problem. In particular, we construct a Laplacian regularized objective function to capture the structure information among clusters. Moreover, considering the importance of the discriminative information underlying in the initial clustering results, we add a discriminative constraint into our proposed objective function. Finally, we verify the performance of the SCE algorithm on both synthetic and real data sets. The experimental results show the effectiveness of our proposed method SCE algorithm.