Robust subspace clustering by Cauchy loss function
Paper and Code
Apr 28, 2019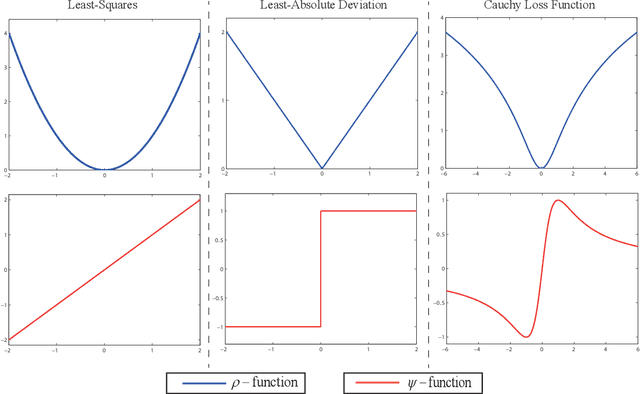


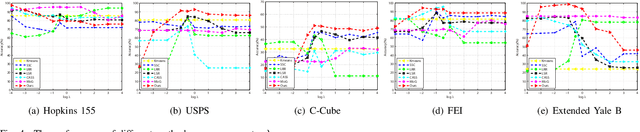
Subspace clustering is a problem of exploring the low-dimensional subspaces of high-dimensional data. State-of-the-arts approaches are designed by following the model of spectral clustering based method. These methods pay much attention to learn the representation matrix to construct a suitable similarity matrix and overlook the influence of the noise term on subspace clustering. However, the real data are always contaminated by the noise and the noise usually has a complicated statistical distribution. To alleviate this problem, we in this paper propose a subspace clustering method based on Cauchy loss function (CLF). Particularly, it uses CLF to penalize the noise term for suppressing the large noise mixed in the real data. This is due to that the CLF's influence function has a upper bound which can alleviate the influence of a single sample, especially the sample with a large noise, on estimating the residuals. Furthermore, we theoretically prove the grouping effect of our proposed method, which means that highly correlated data can be grouped together. Finally, experimental results on five real datasets reveal that our proposed method outperforms several representative clustering methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge