Qingtao Zhao
Online Reinforcement Learning Control by Direct Heuristic Dynamic Programming: from Time-Driven to Event-Driven
Jun 16, 2020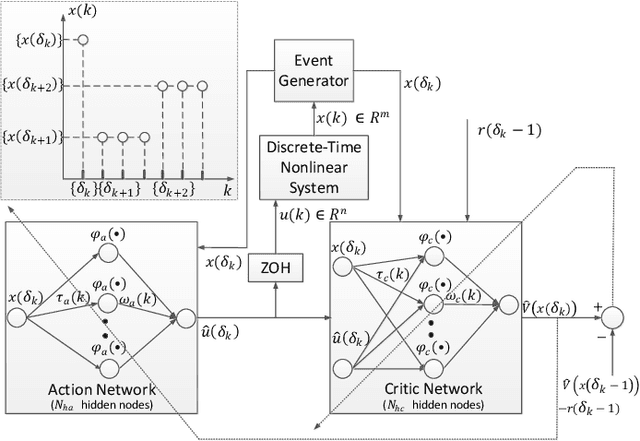
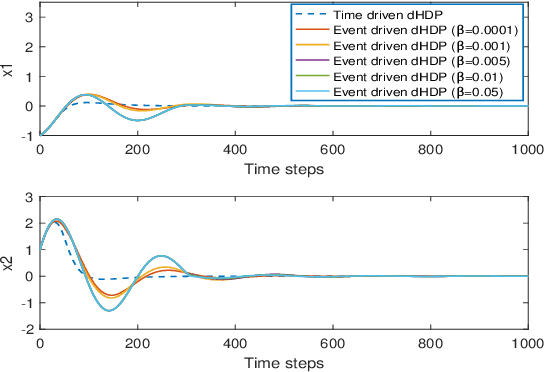
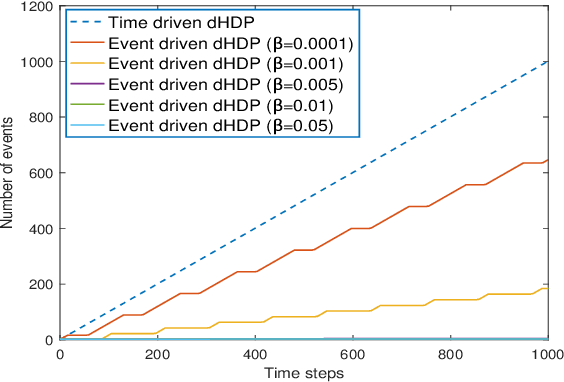
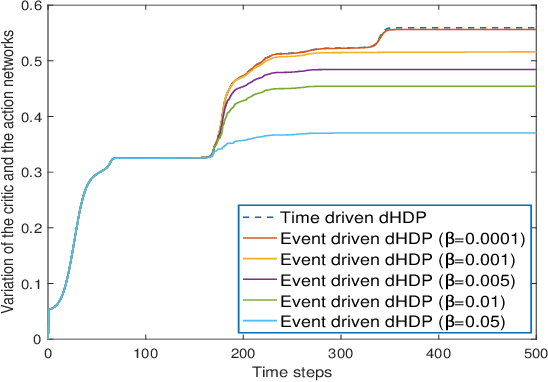
Abstract:In this paper time-driven learning refers to the machine learning method that updates parameters in a prediction model continuously as new data arrives. Among existing approximate dynamic programming (ADP) and reinforcement learning (RL) algorithms, the direct heuristic dynamic programming (dHDP) has been shown an effective tool as demonstrated in solving several complex learning control problems. It continuously updates the control policy and the critic as system states continuously evolve. It is therefore desirable to prevent the time-driven dHDP from updating due to insignificant system event such as noise. Toward this goal, we propose a new event-driven dHDP. By constructing a Lyapunov function candidate, we prove the uniformly ultimately boundedness (UUB) of the system states and the weights in the critic and the control policy networks. Consequently we show the approximate control and cost-to-go function approaching Bellman optimality within a finite bound. We also illustrate how the event-driven dHDP algorithm works in comparison to the original time-driven dHDP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge