Syndicated Bandits: A Framework for Auto Tuning Hyper-parameters in Contextual Bandit Algorithms

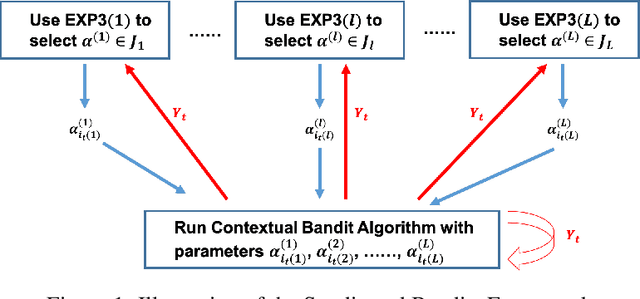
The stochastic contextual bandit problem, which models the trade-off between exploration and exploitation, has many real applications, including recommender systems, online advertising and clinical trials. As many other machine learning algorithms, contextual bandit algorithms often have one or more hyper-parameters. As an example, in most optimal stochastic contextual bandit algorithms, there is an unknown exploration parameter which controls the trade-off between exploration and exploitation. A proper choice of the hyper-parameters is essential for contextual bandit algorithms to perform well. However, it is infeasible to use offline tuning methods to select hyper-parameters in contextual bandit environment since there is no pre-collected dataset and the decisions have to be made in real time. To tackle this problem, we first propose a two-layer bandit structure for auto tuning the exploration parameter and further generalize it to the Syndicated Bandits framework which can learn multiple hyper-parameters dynamically in contextual bandit environment. We show our Syndicated Bandits framework can achieve the optimal regret upper bounds and is general enough to handle the tuning tasks in many popular contextual bandit algorithms, such as LinUCB, LinTS, UCB-GLM, etc. Experiments on both synthetic and real datasets validate the effectiveness of our proposed framework.

Robust Stochastic Linear Contextual Bandits Under Adversarial Attacks

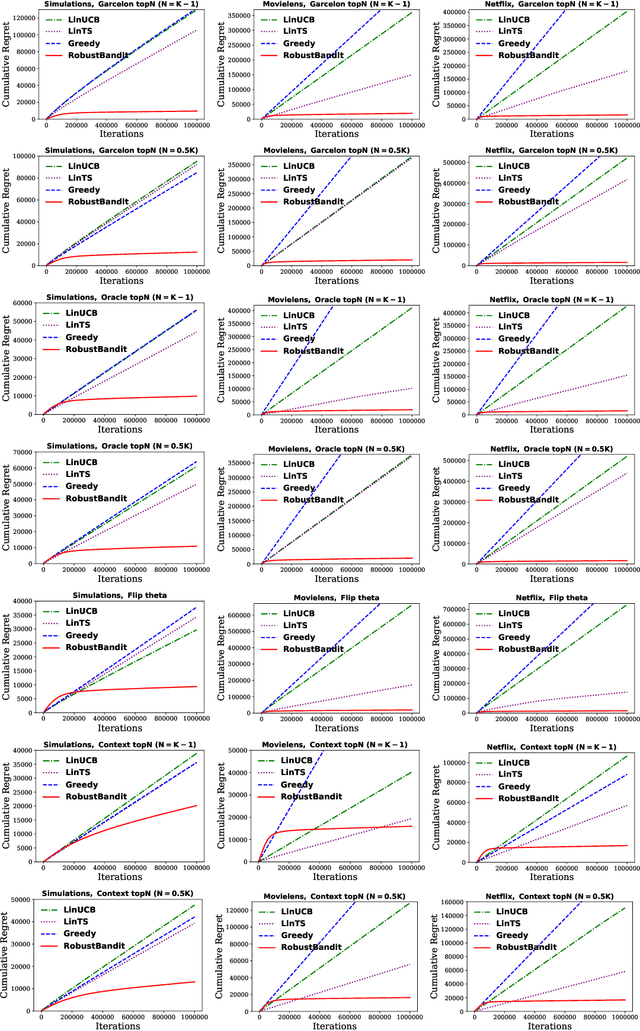
Stochastic linear contextual bandit algorithms have substantial applications in practice, such as recommender systems, online advertising, clinical trials, etc. Recent works show that optimal bandit algorithms are vulnerable to adversarial attacks and can fail completely in the presence of attacks. Existing robust bandit algorithms only work for the non-contextual setting under the attack of rewards and cannot improve the robustness in the general and popular contextual bandit environment. In addition, none of the existing methods can defend against attacked context. In this work, we provide the first robust bandit algorithm for stochastic linear contextual bandit setting under a fully adaptive and omniscient attack. Our algorithm not only works under the attack of rewards, but also under attacked context. Moreover, it does not need any information about the attack budget or the particular form of the attack. We provide theoretical guarantees for our proposed algorithm and show by extensive experiments that our proposed algorithm significantly improves the robustness against various kinds of popular attacks.

An Efficient Algorithm For Generalized Linear Bandit: Online Stochastic Gradient Descent and Thompson Sampling

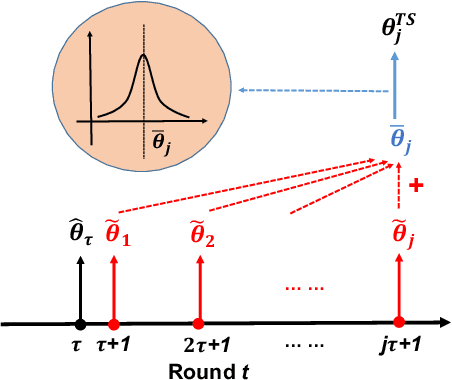
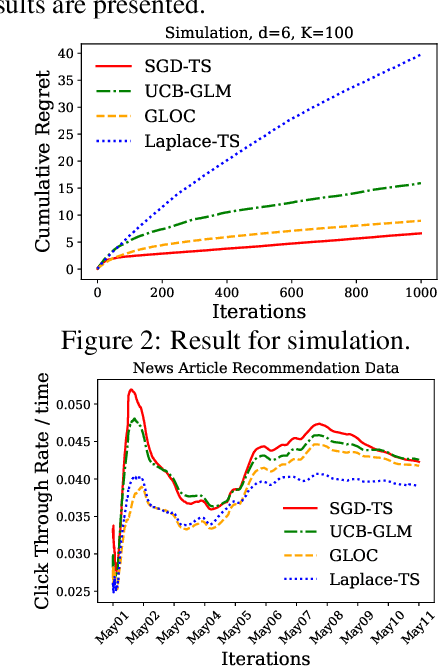
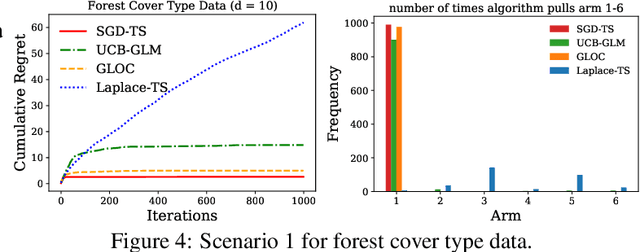
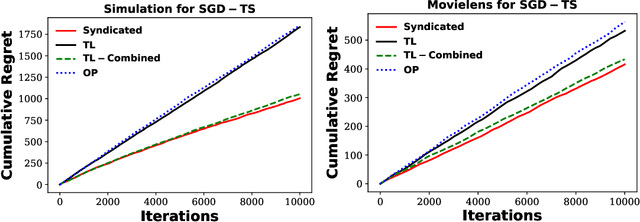
We consider the contextual bandit problem, where a player sequentially makes decisions based on past observations to maximize the cumulative reward. Although many algorithms have been proposed for contextual bandit, most of them rely on finding the maximum likelihood estimator at each iteration, which requires $O(t)$ time at the $t$-th iteration and are memory inefficient. A natural way to resolve this problem is to apply online stochastic gradient descent (SGD) so that the per-step time and memory complexity can be reduced to constant with respect to $t$, but a contextual bandit policy based on online SGD updates that balances exploration and exploitation has remained elusive. In this work, we show that online SGD can be applied to the generalized linear bandit problem. The proposed SGD-TS algorithm, which uses a single-step SGD update to exploit past information and uses Thompson Sampling for exploration, achieves $\tilde{O}(\sqrt{dT})$ regret with the total time complexity that scales linearly in $T$ and $d$, where $T$ is the total number of rounds and $d$ is the number of features. Experimental results show that SGD-TS consistently outperforms existing algorithms on both synthetic and real datasets.

Multiscale Non-stationary Stochastic Bandits

Classic contextual bandit algorithms for linear models, such as LinUCB, assume that the reward distribution for an arm is modeled by a stationary linear regression. When the linear regression model is non-stationary over time, the regret of LinUCB can scale linearly with time. In this paper, we propose a novel multiscale changepoint detection method for the non-stationary linear bandit problems, called Multiscale-LinUCB, which actively adapts to the changing environment. We also provide theoretical analysis of regret bound for Multiscale-LinUCB algorithm. Experimental results show that our proposed Multiscale-LinUCB algorithm outperforms other state-of-the-art algorithms in non-stationary contextual environments.