Low-resolution Prior Equilibrium Network for CT Reconstruction

The unrolling method has been investigated for learning variational models in X-ray computed tomography. However, it has been observed that directly unrolling the regularization model through gradient descent does not produce satisfactory results. In this paper, we present a novel deep learning-based CT reconstruction model, where the low-resolution image is introduced to obtain an effective regularization term for improving the network`s robustness. Our approach involves constructing the backbone network architecture by algorithm unrolling that is realized using the deep equilibrium architecture. We theoretically discuss the convergence of the proposed low-resolution prior equilibrium model and provide the conditions to guarantee convergence. Experimental results on both sparse-view and limited-angle reconstruction problems are provided, demonstrating that our end-to-end low-resolution prior equilibrium model outperforms other state-of-the-art methods in terms of noise reduction, contrast-to-noise ratio, and preservation of edge details.

Curvature regularization for Non-line-of-sight Imaging from Under-sampled Data

Non-line-of-sight (NLOS) imaging aims to reconstruct the three-dimensional hidden scenes from the data measured in the line-of-sight, which uses photon time-of-flight information encoded in light after multiple diffuse reflections. The under-sampled scanning data can facilitate fast imaging. However, the resulting reconstruction problem becomes a serious ill-posed inverse problem, the solution of which is of high possibility to be degraded due to noises and distortions. In this paper, we propose two novel NLOS reconstruction models based on curvature regularization, i.e., the object-domain curvature regularization model and the dual (i.e., signal and object)-domain curvature regularization model. Fast numerical optimization algorithms are developed relying on the alternating direction method of multipliers (ADMM) with the backtracking stepsize rule, which are further accelerated by GPU implementation. We evaluate the proposed algorithms on both synthetic and real datasets, which achieve state-of-the-art performance, especially in the compressed sensing setting. All our codes and data are available at https://github.com/Duanlab123/CurvNLOS.

LRIP-Net: Low-Resolution Image Prior based Network for Limited-Angle CT Reconstruction

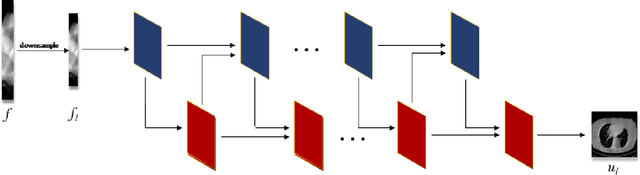
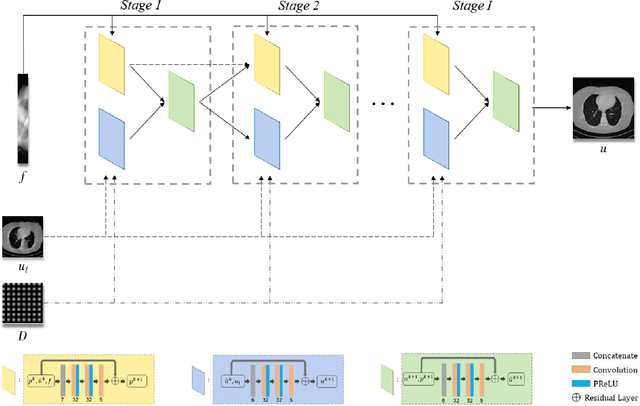
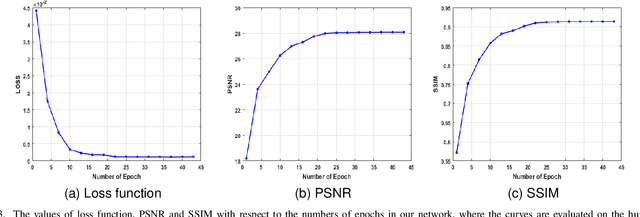
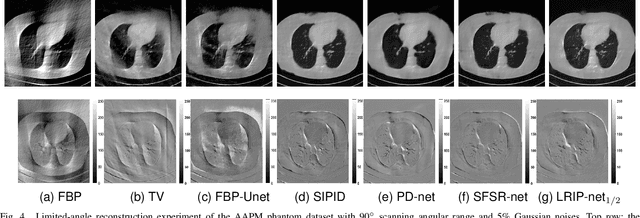
In the practical applications of computed tomography imaging, the projection data may be acquired within a limited-angle range and corrupted by noises due to the limitation of scanning conditions. The noisy incomplete projection data results in the ill-posedness of the inverse problems. In this work, we theoretically verify that the low-resolution reconstruction problem has better numerical stability than the high-resolution problem. In what follows, a novel low-resolution image prior based CT reconstruction model is proposed to make use of the low-resolution image to improve the reconstruction quality. More specifically, we build up a low-resolution reconstruction problem on the down-sampled projection data, and use the reconstructed low-resolution image as prior knowledge for the original limited-angle CT problem. We solve the constrained minimization problem by the alternating direction method with all subproblems approximated by the convolutional neural networks. Numerical experiments demonstrate that our double-resolution network outperforms both the variational method and popular learning-based reconstruction methods on noisy limited-angle reconstruction problems.