LRIP-Net: Low-Resolution Image Prior based Network for Limited-Angle CT Reconstruction
Paper and Code
Jul 30, 2022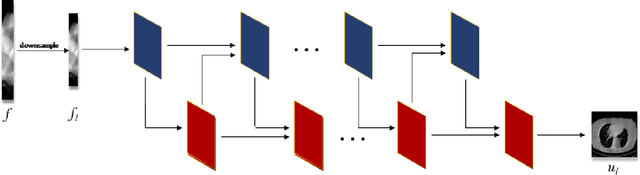
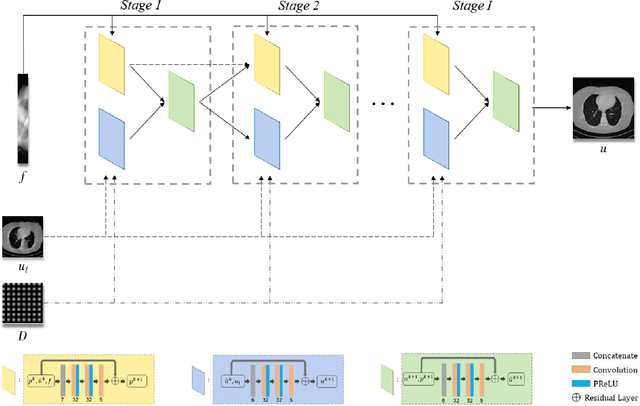
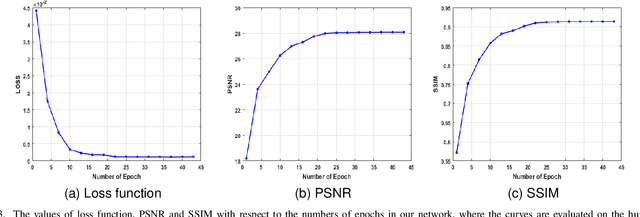
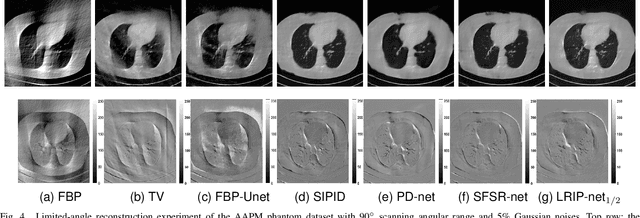
In the practical applications of computed tomography imaging, the projection data may be acquired within a limited-angle range and corrupted by noises due to the limitation of scanning conditions. The noisy incomplete projection data results in the ill-posedness of the inverse problems. In this work, we theoretically verify that the low-resolution reconstruction problem has better numerical stability than the high-resolution problem. In what follows, a novel low-resolution image prior based CT reconstruction model is proposed to make use of the low-resolution image to improve the reconstruction quality. More specifically, we build up a low-resolution reconstruction problem on the down-sampled projection data, and use the reconstructed low-resolution image as prior knowledge for the original limited-angle CT problem. We solve the constrained minimization problem by the alternating direction method with all subproblems approximated by the convolutional neural networks. Numerical experiments demonstrate that our double-resolution network outperforms both the variational method and popular learning-based reconstruction methods on noisy limited-angle reconstruction problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge