Machine learning predictions for local electronic properties of disordered correlated electron systems

We present a scalable machine learning (ML) model to predict local electronic properties such as on-site electron number and double occupation for disordered correlated electron systems. Our approach is based on the locality principle, or the nearsightedness nature, of many-electron systems, which means local electronic properties depend mainly on the immediate environment. A ML model is developed to encode this complex dependence of local quantities on the neighborhood. We demonstrate our approach using the square-lattice Anderson-Hubbard model, which is a paradigmatic system for studying the interplay between Mott transition and Anderson localization. We develop a lattice descriptor based on group-theoretical method to represent the on-site random potentials within a finite region. The resultant feature variables are used as input to a multi-layer fully connected neural network, which is trained from datasets of variational Monte Carlo (VMC) simulations on small systems. We show that the ML predictions agree reasonably well with the VMC data. Our work underscores the promising potential of ML methods for multi-scale modeling of correlated electron systems.

Descriptors for Machine Learning Model of Generalized Force Field in Condensed Matter Systems

We outline the general framework of machine learning (ML) methods for multi-scale dynamical modeling of condensed matter systems, and in particular of strongly correlated electron models. Complex spatial temporal behaviors in these systems often arise from the interplay between quasi-particles and the emergent dynamical classical degrees of freedom, such as local lattice distortions, spins, and order-parameters. Central to the proposed framework is the ML energy model that, by successfully emulating the time-consuming electronic structure calculation, can accurately predict a local energy based on the classical field in the intermediate neighborhood. In order to properly include the symmetry of the electron Hamiltonian, a crucial component of the ML energy model is the descriptor that transforms the neighborhood configuration into invariant feature variables, which are input to the learning model. A general theory of the descriptor for the classical fields is formulated, and two types of models are distinguished depending on the presence or absence of an internal symmetry for the classical field. Several specific approaches to the descriptor of the classical fields are presented. Our focus is on the group-theoretical method that offers a systematic and rigorous approach to compute invariants based on the bispectrum coefficients. We propose an efficient implementation of the bispectrum method based on the concept of reference irreducible representations. Finally, the implementations of the various descriptors are demonstrated on well-known electronic lattice models.

Machine learning nonequilibrium electron forces for adiabatic spin dynamics

We present a generalized potential theory of nonequilibrium torques for the Landau-Lifshitz equation. The general formulation of exchange forces in terms of two potential energies allows for the implementation of accurate machine learning models for adiabatic spin dynamics of out-of-equilibrium itinerant magnetic systems. To demonstrate our approach, we develop a deep-learning neural network that successfully learns the forces in a driven s-d model computed from the nonequilibrium Green's function method. We show that the Landau-Lifshitz dynamics simulations with forces predicted from the neural-net model accurately reproduce the voltage-driven domain-wall propagation. Our work opens a new avenue for multi-scale modeling of nonequilibrium dynamical phenomena in itinerant magnets and spintronics based on machine-learning models.

Anomalous phase separation and hidden coarsening of super-clusters in the Falicov-Kimball model

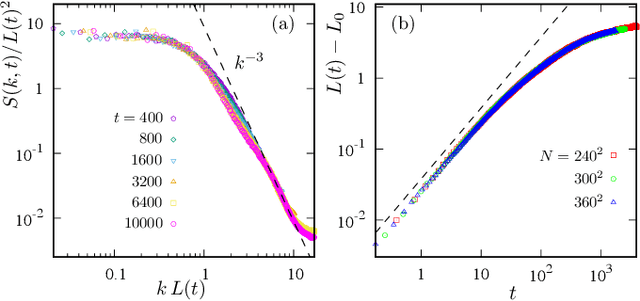
We show that the celebrated Falicov-Kimball model exhibits rich and intriguing phase-ordering dynamics. Applying modern machine learning methods to enable large-scale quantum kinetic Monte Carlo simulations, we uncover an unusual phase-separation scenario in which the growth of charge checkerboard clusters competes with domain coarsening related to a hidden symmetry-breaking. A self-trapping mechanism as a result of this competition gives rise to arrested growth of checkerboard patterns and their super-clusters. Glassy behaviors similar to the one reported in this work could be generic for other correlated electron systems.

Arrested phase separation in double-exchange models: machine-learning enabled large-scale simulation

We present large-scale dynamical simulations of electronic phase separation in the single-band double-exchange model based on deep-learning neural-network potentials trained from small-size exact diagonalization solutions. We uncover an intriguing correlation-induced freezing behavior as doped holes are segregated from half-filled insulating background during equilibration. While the aggregation of holes is stabilized by the formation of ferromagnetic clusters through Hund's coupling between charge carriers and local magnetic moments, this stabilization also creates confining potentials for holes when antiferromagnetic spin-spin correlation is well developed in the background. The dramatically reduced mobility of the self-trapped holes prematurely disrupts further growth of the ferromagnetic clusters, leading to an arrested phase separation. Implications of our findings for phase separation dynamics in materials that exhibit colossal magnetoresistance effect are discussed.

Machine learning dynamics of phase separation in correlated electron magnets

We demonstrate machine-learning enabled large-scale dynamical simulations of electronic phase separation in double-exchange system. This model, also known as the ferromagnetic Kondo lattice model, is believed to be relevant for the colossal magnetoresistance phenomenon. Real-space simulations of such inhomogeneous states with exchange forces computed from the electron Hamiltonian can be prohibitively expensive for large systems. Here we show that linear-scaling exchange field computation can be achieved using neural networks trained by datasets from exact calculation on small lattices. Our Landau-Lifshitz dynamics simulations based on machine-learning potentials nicely reproduce not only the nonequilibrium relaxation process, but also correlation functions that agree quantitatively with exact simulations. Our work paves the way for large-scale dynamical simulations of correlated electron systems using machine-learning models.