Relationship-aware Multivariate Sampling Strategy for Scientific Simulation Data

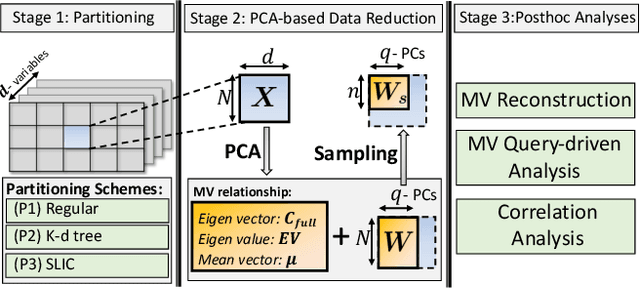
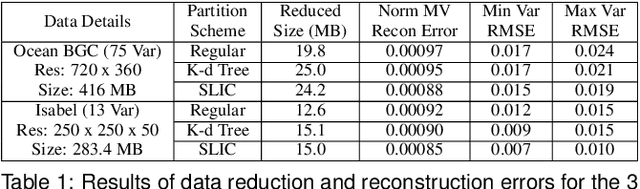
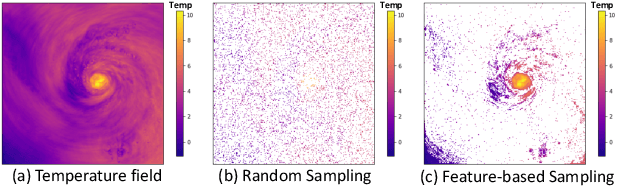
With the increasing computational power of current supercomputers, the size of data produced by scientific simulations is rapidly growing. To reduce the storage footprint and facilitate scalable post-hoc analyses of such scientific data sets, various data reduction/summarization methods have been proposed over the years. Different flavors of sampling algorithms exist to sample the high-resolution scientific data, while preserving important data properties required for subsequent analyses. However, most of these sampling algorithms are designed for univariate data and cater to post-hoc analyses of single variables. In this work, we propose a multivariate sampling strategy which preserves the original variable relationships and enables different multivariate analyses directly on the sampled data. Our proposed strategy utilizes principal component analysis to capture the variance of multivariate data and can be built on top of any existing state-of-the-art sampling algorithms for single variables. In addition, we also propose variants of different data partitioning schemes (regular and irregular) to efficiently model the local multivariate relationships. Using two real-world multivariate data sets, we demonstrate the efficacy of our proposed multivariate sampling strategy with respect to its data reduction capabilities as well as the ease of performing efficient post-hoc multivariate analyses.

Coarse-Grain Cluster Analysis of Tensors With Application to Climate Biome Identification

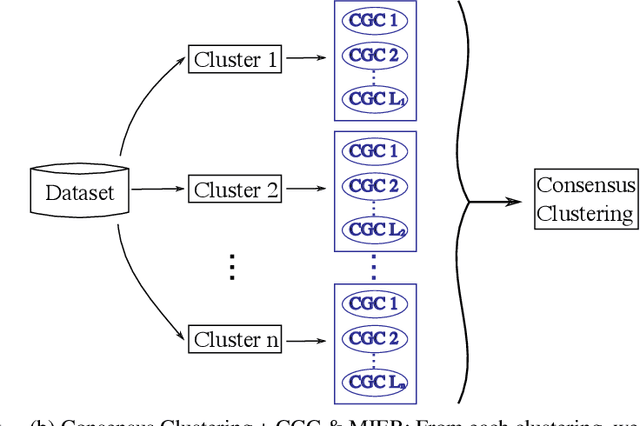
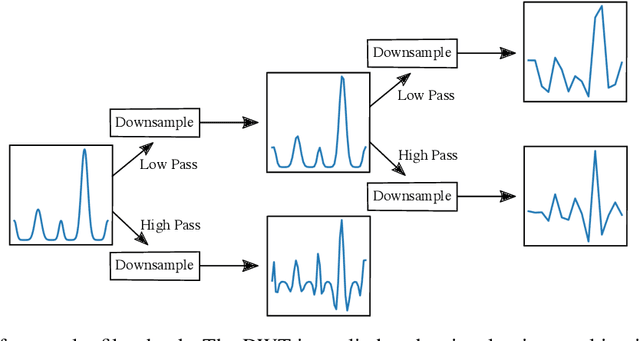
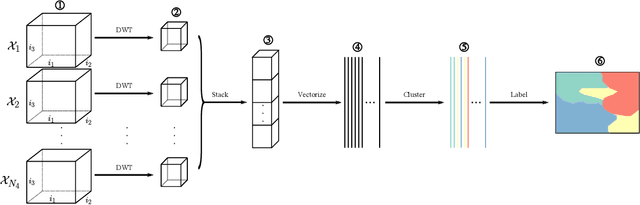
A tensor provides a concise way to codify the interdependence of complex data. Treating a tensor as a d-way array, each entry records the interaction between the different indices. Clustering provides a way to parse the complexity of the data into more readily understandable information. Clustering methods are heavily dependent on the algorithm of choice, as well as the chosen hyperparameters of the algorithm. However, their sensitivity to data scales is largely unknown. In this work, we apply the discrete wavelet transform to analyze the effects of coarse-graining on clustering tensor data. We are particularly interested in understanding how scale effects clustering of the Earth's climate system. The discrete wavelet transform allows classification of the Earth's climate across a multitude of spatial-temporal scales. The discrete wavelet transform is used to produce an ensemble of classification estimates, as opposed to a single classification. Using information theory, we discover a sub-collection of the ensemble that span the majority of the variance observed, allowing for efficient consensus clustering techniques that can be used to identify climate biomes.