Coarse-Grain Cluster Analysis of Tensors With Application to Climate Biome Identification
Paper and Code
Jan 22, 2020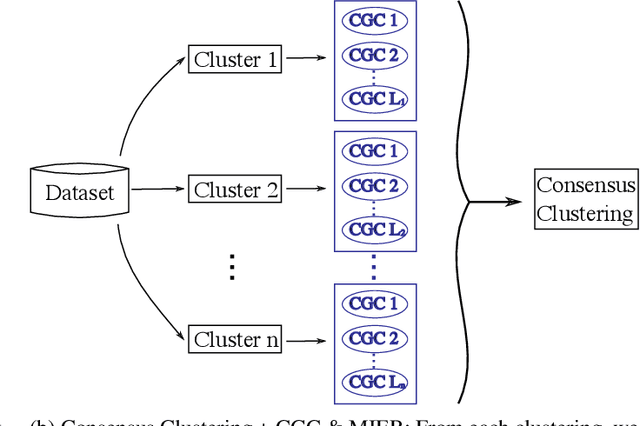
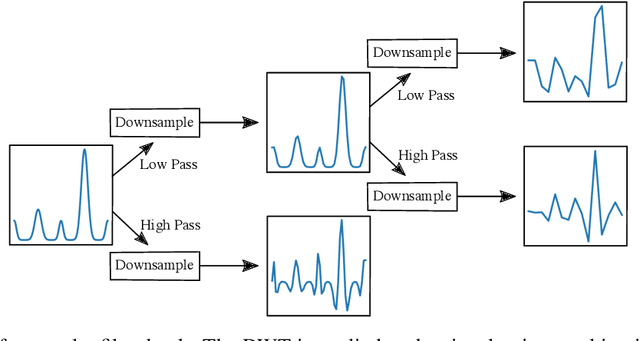
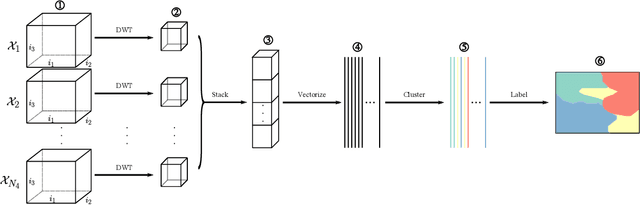

A tensor provides a concise way to codify the interdependence of complex data. Treating a tensor as a d-way array, each entry records the interaction between the different indices. Clustering provides a way to parse the complexity of the data into more readily understandable information. Clustering methods are heavily dependent on the algorithm of choice, as well as the chosen hyperparameters of the algorithm. However, their sensitivity to data scales is largely unknown. In this work, we apply the discrete wavelet transform to analyze the effects of coarse-graining on clustering tensor data. We are particularly interested in understanding how scale effects clustering of the Earth's climate system. The discrete wavelet transform allows classification of the Earth's climate across a multitude of spatial-temporal scales. The discrete wavelet transform is used to produce an ensemble of classification estimates, as opposed to a single classification. Using information theory, we discover a sub-collection of the ensemble that span the majority of the variance observed, allowing for efficient consensus clustering techniques that can be used to identify climate biomes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge