A Versatile Multi-Robot Monte Carlo Tree Search Planner for On-Line Coverage Path Planning

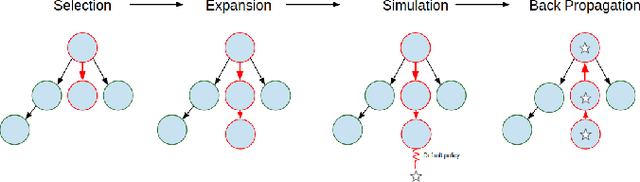
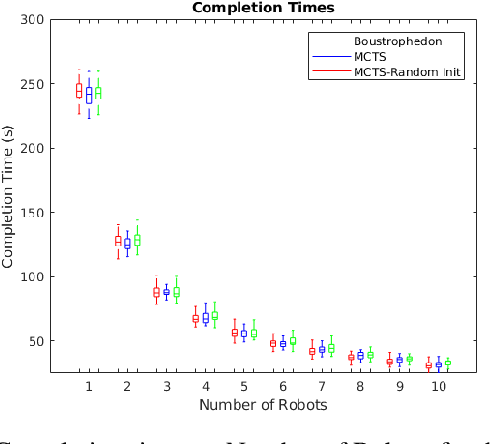
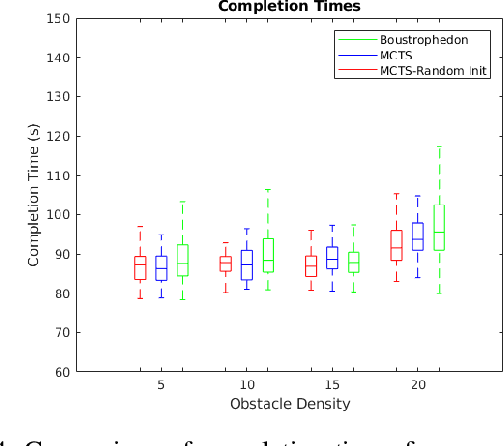
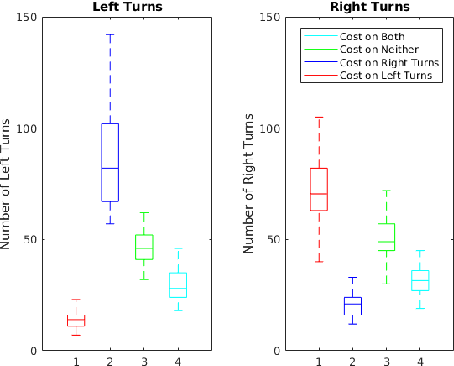
Mobile robots hold great promise in reducing the need for humans to perform jobs such as vacuuming, seeding,harvesting, painting, search and rescue, and inspection. In practice, these tasks must often be done without an exact map of the area and could be completed more quickly through the use of multiple robots working together. The task of simultaneously covering and mapping an area with multiple robots is known as multi-robot on-line coverage and is a growing area of research. Many multi-robot on-line coverage path planning algorithms have been developed as extensions of well established off-line coverage algorithms. In this work we introduce a novel approach to multi-robot on-line coverage path planning based on a method borrowed from game theory and machine learning- Monte Carlo Tree Search. We implement a Monte Carlo Tree Search planner and compare completion times against a Boustrophedon-based on-line multi-robot planner. The MCTS planner is shown to perform on par with the conventional Boustrophedon algorithm in simulations varying the number of robots and the density of obstacles in the map. The versatility of the MCTS planner is demonstrated by incorporating secondary objectives such as turn minimization while performing the same coverage task. The versatility of the MCTS planner suggests it is well suited to many multi-objective tasks that arise in mobile robotics.

Parameterized and GPU-Parallelized Real-Time Model Predictive Control for High Degree of Freedom Robots

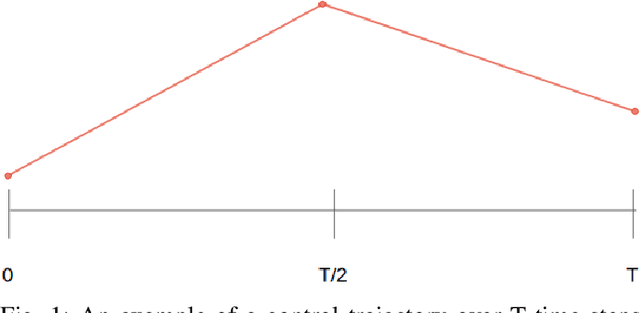
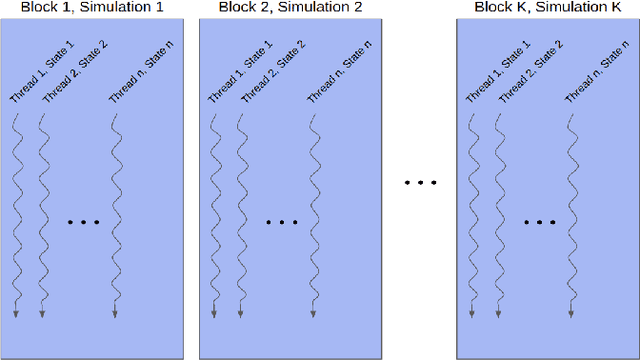
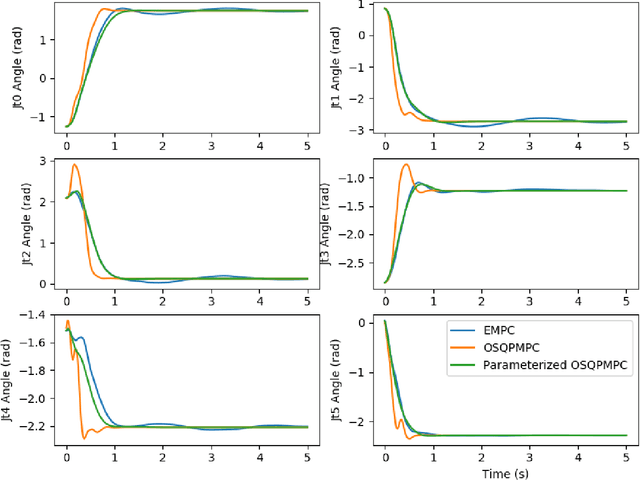
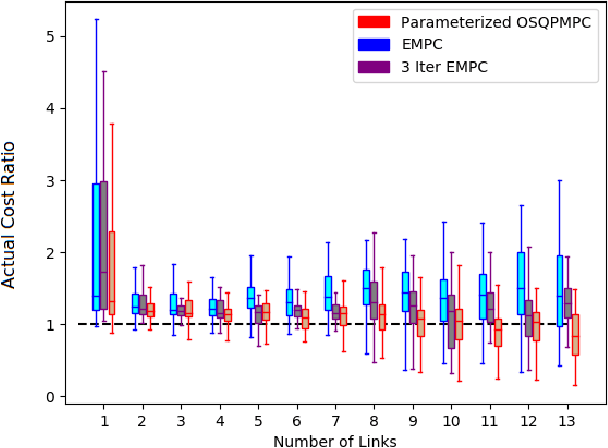
This work presents and evaluates a novel input parameterization method which improves the tractability of model predictive control (MPC) for high degree of freedom (DoF) robots. Experimental results demonstrate that by parameterizing the input trajectory more than three quarters of the optimization variables used in traditional MPC can be eliminated with practically no effect on system performance. This parameterization also leads to trajectories which are more conservative, producing less overshoot in underdamped systems with modeling error. In this paper we present two MPC solution methods that make use of this parameterization. The first uses a convex solver, and the second makes use of parallel computing on a graphics processing unit (GPU). We show that both approaches drastically reduce solve times for large DoF, long horizon MPC problems allowing solutions at real-time rates. Through simulation and hardware experiments, we show that the parameterized convex solver MPC has faster solve times than traditional MPC for high DoF cases while still achieving similar performance. For the GPU-based MPC solution method, we use an evolutionary algorithm and that we call Evolutionary MPC (EMPC). EMPC is shown to have even faster solve times for high DoF systems. Solve times for EMPC are shown to decrease even further through the use of a more powerful GPU. This suggests that parallelized MPC methods will become even more advantageous with the improvement and prevalence of GPU technology.