Asset price movement prediction using empirical mode decomposition and Gaussian mixture models

We investigated the use of Empirical Mode Decomposition (EMD) combined with Gaussian Mixture Models (GMM), feature engineering and machine learning algorithms to optimize trading decisions. We used five, two, and one year samples of hourly candle data for GameStop, Tesla, and XRP (Ripple) markets respectively. Applying a 15 hour rolling window for each market, we collected several features based on a linear model and other classical features to predict the next hour's movement. Subsequently, a GMM filtering approach was used to identify clusters among these markets. For each cluster, we applied the EMD algorithm to extract high, medium, low and trend components from each feature collected. A simple thresholding algorithm was applied to classify market movements based on the percentage change in each market's close price. We then evaluated the performance of various machine learning models, including Random Forests (RF) and XGBoost, in classifying market movements. A naive random selection of trading decisions was used as a benchmark, which assumed equal probabilities for each outcome, and a temporal cross-validation approach was used to test models on 40%, 30%, and 20% of the dataset. Our results indicate that transforming selected features using EMD improves performance, particularly for ensemble learning algorithms like Random Forest and XGBoost, as measured by accumulated profit. Finally, GMM filtering expanded the range of learning algorithm and data source combinations that outperformed the top percentile of the random baseline.

A Computational Theory of Subjective Probability

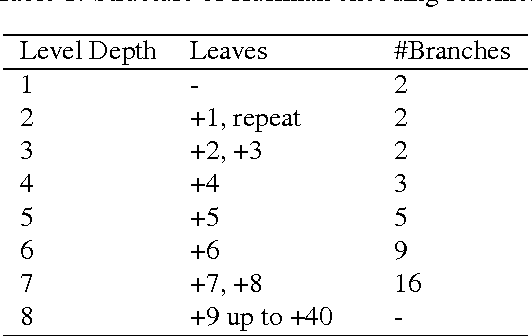
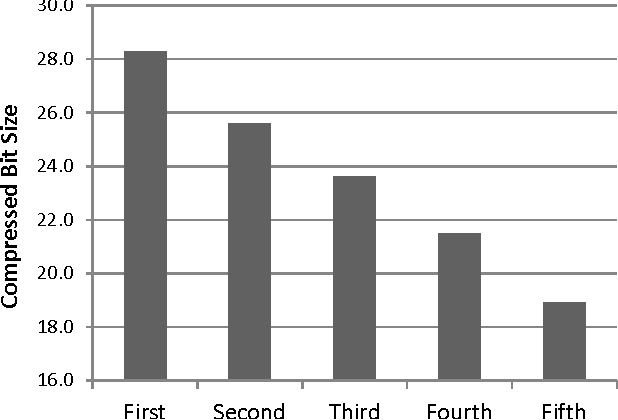
In this article we demonstrate how algorithmic probability theory is applied to situations that involve uncertainty. When people are unsure of their model of reality, then the outcome they observe will cause them to update their beliefs. We argue that classical probability cannot be applied in such cases, and that subjective probability must instead be used. In Experiment 1 we show that, when judging the probability of lottery number sequences, people apply subjective rather than classical probability. In Experiment 2 we examine the conjunction fallacy and demonstrate that the materials used by Tversky and Kahneman (1983) involve model uncertainty. We then provide a formal mathematical proof that, for every uncertain model, there exists a conjunction of outcomes which is more subjectively probable than either of its constituents in isolation.