Accurate brain extraction using Active Shape Model and Convolutional Neural Networks

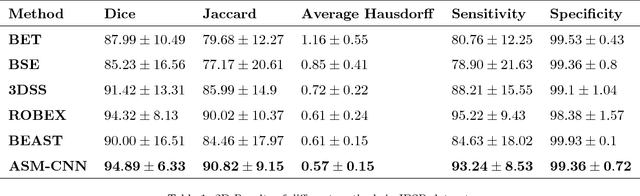
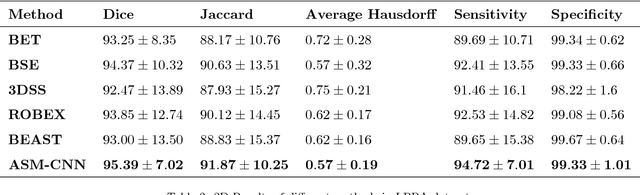
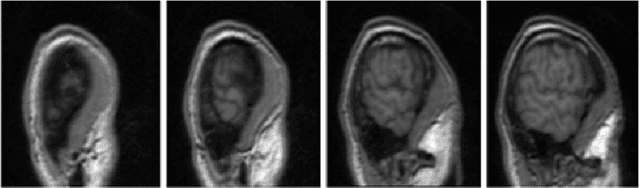
Brain extraction or skull stripping is a fundamental procedure in most of neuroimaging processing systems. The performance of this procedure has had a critical impact on the success of neuroimaging analysis. After several years of research and development, brain extraction still remains a challenging problem. In this paper, we propose an effective method for skull stripping in Magnetic Resonance Imaging (MRI) scans named ASM-CNN. Our system is a combination of Active Shape Model (ASM) and Convolutional Neural Network (CNN), taking full advantage of these two methods to achieve remarkable results. Instead of working with 3D structures, we process 2D image sequences in sagittal plane. First, we divide images into different groups such that, in each group, the shapes and structures of brain boundaries have similar appearances. This allows developing precise algorithms for each group in order to produce high performance segmentation results. Second, a modified version of ASM is used to detect the brain boundary in images by utilizing prior knowledge of each group. Finally, CNN and the post-processing methods such as Conditional Random Field, Gaussian Process and some special rules are applied to refine segmentation contour produced by ASM. We compared ASM-CNN with the latest version of five state-of-the-art, publicly available methods, namely BET, BSE, 3DSS, ROBEX and BEAST. The evaluation was carried out by using three public datasets IBSR, LPBA and OASIS. The experimental results show that the proposed method outperforms five states-of-the-art algorithms, surpassing all the other methods by a significant margin in all experiments.

Complex Matrix Factorization for Face Recognition

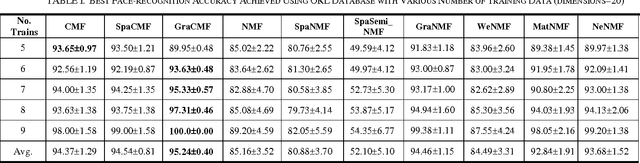
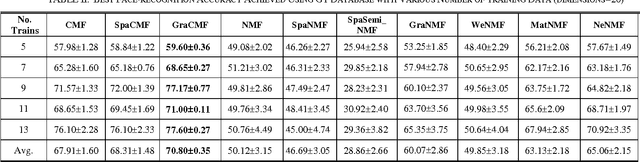
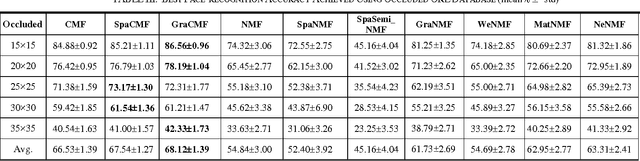
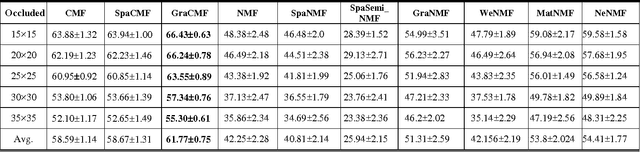
This work developed novel complex matrix factorization methods for face recognition; the methods were complex matrix factorization (CMF), sparse complex matrix factorization (SpaCMF), and graph complex matrix factorization (GraCMF). After real-valued data are transformed into a complex field, the complex-valued matrix will be decomposed into two matrices of bases and coefficients, which are derived from solutions to an optimization problem in a complex domain. The generated objective function is the real-valued function of the reconstruction error, which produces a parametric description. Factorizing the matrix of complex entries directly transformed the constrained optimization problem into an unconstrained optimization problem. Additionally, a complex vector space with N dimensions can be regarded as a 2N-dimensional real vector space. Accordingly, all real analytic properties can be exploited in the complex field. The ability to exploit these important characteristics motivated the development herein of a simpler framework that can provide better recognition results. The effectiveness of this framework will be clearly elucidated in later sections in this paper.