Complex Matrix Factorization for Face Recognition
Paper and Code
Dec 08, 2016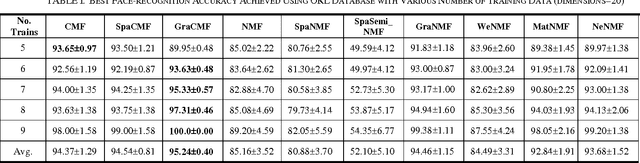
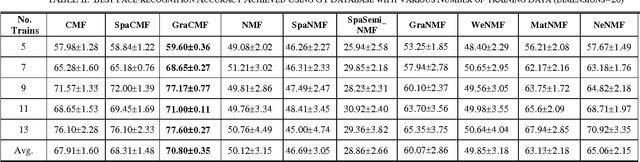
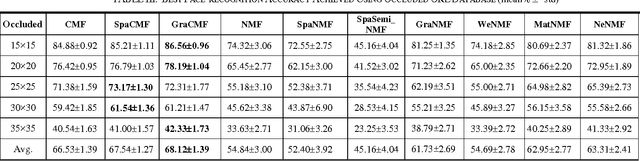
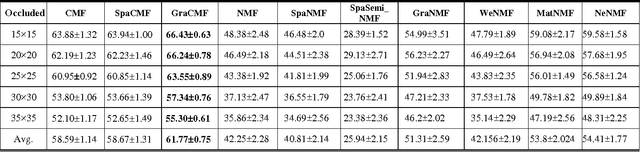
This work developed novel complex matrix factorization methods for face recognition; the methods were complex matrix factorization (CMF), sparse complex matrix factorization (SpaCMF), and graph complex matrix factorization (GraCMF). After real-valued data are transformed into a complex field, the complex-valued matrix will be decomposed into two matrices of bases and coefficients, which are derived from solutions to an optimization problem in a complex domain. The generated objective function is the real-valued function of the reconstruction error, which produces a parametric description. Factorizing the matrix of complex entries directly transformed the constrained optimization problem into an unconstrained optimization problem. Additionally, a complex vector space with N dimensions can be regarded as a 2N-dimensional real vector space. Accordingly, all real analytic properties can be exploited in the complex field. The ability to exploit these important characteristics motivated the development herein of a simpler framework that can provide better recognition results. The effectiveness of this framework will be clearly elucidated in later sections in this paper.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge