Defensive Alliances in Signed Networks

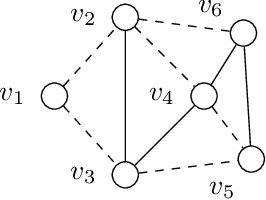
The analysis of (social) networks and multi-agent systems is a central theme in Artificial Intelligence. Some line of research deals with finding groups of agents that could work together to achieve a certain goal. To this end, different notions of so-called clusters or communities have been introduced in the literature of graphs and networks. Among these, defensive alliance is a kind of quantitative group structure. However, all studies on the alliance so for have ignored one aspect that is central to the formation of alliances on a very intuitive level, assuming that the agents are preconditioned concerning their attitude towards other agents: they prefer to be in some group (alliance) together with the agents they like, so that they are happy to help each other towards their common aim, possibly then working against the agents outside of their group that they dislike. Signed networks were introduced in the psychology literature to model liking and disliking between agents, generalizing graphs in a natural way. Hence, we propose the novel notion of a defensive alliance in the context of signed networks. We then investigate several natural algorithmic questions related to this notion. These, and also combinatorial findings, connect our notion to that of correlation clustering, which is a well-established idea of finding groups of agents within a signed network. Also, we introduce a new structural parameter for signed graphs, signed neighborhood diversity snd, and exhibit a parameterized algorithm that finds a smallest defensive alliance in a signed graph.

Heuristic for Diverse Kemeny Rank Aggregation based on Quantum Annealing

The Kemeny Rank Aggregation (KRA) problem is a well-studied problem in the field of Social Choice with a variety of applications in many different areas like databases and search engines. Intuitively, given a set of votes over a set of candidates, the problem asks to find an aggregated ranking of candidates that minimizes the overall dissatisfaction concerning the votes. Recently, a diverse version of KRA was considered which asks for a sufficiently diverse set of sufficiently good solutions. The framework of diversity of solutions is a young and thriving topic in the field of artificial intelligence. The main idea is to provide the user with not just one, but with a set of different solutions, enabling her to pick a sufficiently good solution that satisfies additional subjective criteria that are hard or impossible to model. In this work, we use a quantum annealer to solve the KRA problem and to compute a representative set of solutions. Quantum annealing is a meta search heuristic that does not only show promising runtime behavior on currently existing prototypes but also samples the solutions space in an inherently different way, making use of quantum effects. We describe how KRA instances can be solved by a quantum annealer and provide an implementation as well as experimental evaluations. As existing quantum annealers are still restricted in their number of qubits, we further implement two different data reduction rules that can split an instance into a set of smaller instances. In our evaluation, we compare classical heuristics that allow to sample multiple solutions such as simulated annealing and local search with quantum annealing performed on a physical quantum annealer. We compare runtime, quality of solution, and diversity of solutions, with and without applying preceding data reduction rules.

Diversity in Kemeny Rank Aggregation: A Parameterized Approach

In its most traditional setting, the main concern of optimization theory is the search for optimal solutions for instances of a given computational problem. A recent trend of research in artificial intelligence, called solution diversity, has focused on the development of notions of optimality that may be more appropriate in settings where subjectivity is essential. The idea is that instead of aiming at the development of algorithms that output a single optimal solution, the goal is to investigate algorithms that output a small set of sufficiently good solutions that are sufficiently diverse from one another. In this way, the user has the opportunity to choose the solution that is most appropriate to the context at hand. It also displays the richness of the solution space. When combined with techniques from parameterized complexity theory, the paradigm of diversity of solutions offers a powerful algorithmic framework to address problems of practical relevance. In this work, we investigate the impact of this combination in the field of Kemeny Rank Aggregation, a well-studied class of problems lying in the intersection of order theory and social choice theory and also in the field of order theory itself. In particular, we show that the Kemeny Rank Aggregation problem is fixed-parameter tractable with respect to natural parameters providing natural formalizations of the notions of diversity and of the notion of a sufficiently good solution. Our main results work both when considering the traditional setting of aggregation over linearly ordered votes, and in the more general setting where votes are partially ordered.

Regular Intersection Emptiness of Graph Problems: Finding a Needle in a Haystack of Graphs with the Help of Automata

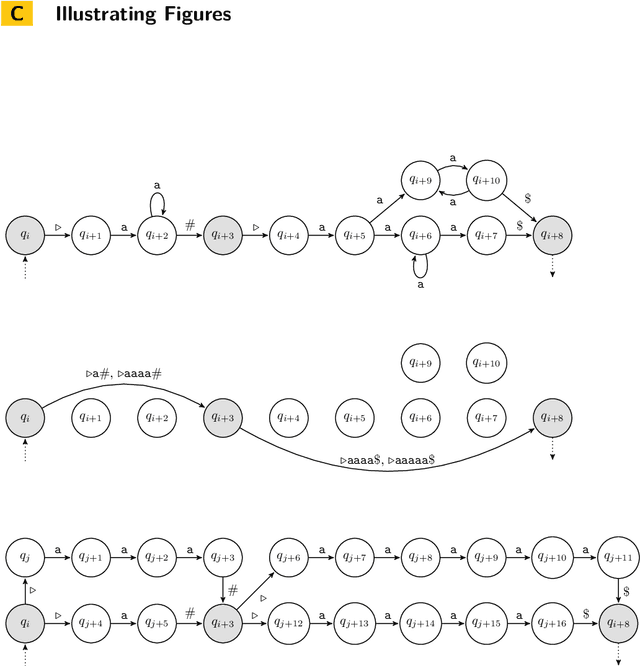
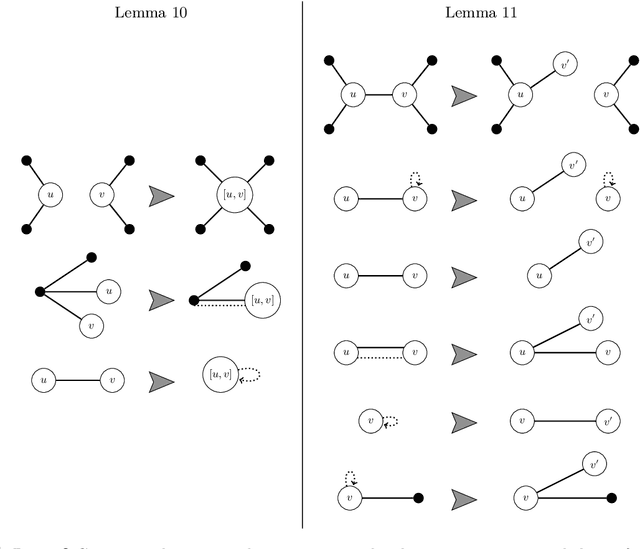
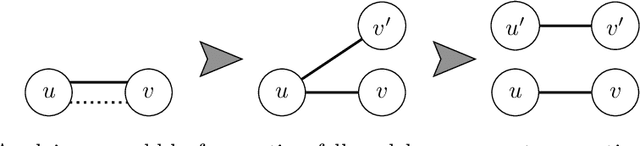
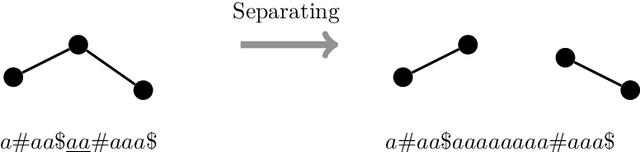
The Int_reg-problem of a combinatorial problem P asks, given a nondeterministic automaton M as input, whether the language L(M) accepted by M contains any positive instance of the problem P. We consider the Int_reg-problem for a number of different graph problems and give general criteria that give decision procedures for these Int_reg-problems. To achieve this goal, we consider a natural graph encoding so that the language of all graph encodings is regular. Then, we draw the connection between classical pumping- and interchange-arguments from the field of formal language theory with the graph operations induced on the encoded graph. Our techniques apply among others to the Int_reg-problem of well-known graph problems like Vertex Cover and Independent Set, as well as to subgraph problems, graph-edit problems and graph-partitioning problems, including coloring problems.