Euclidean Equivariant Models for Generative Graphical Inverse Kinematics

Quickly and reliably finding accurate inverse kinematics (IK) solutions remains a challenging problem for robotic manipulation. Existing numerical solvers typically produce a single solution only and rely on local search techniques to minimize a highly nonconvex objective function. Recently, learning-based approaches that approximate the entire feasible set of solutions have shown promise as a means to generate multiple fast and accurate IK results in parallel. However, existing learning-based techniques have a significant drawback: each robot of interest requires a specialized model that must be trained from scratch. To address this shortcoming, we investigate a novel distance-geometric robot representation coupled with a graph structure that allows us to leverage the flexibility of graph neural networks (GNNs). We use this approach to train a generative graphical inverse kinematics solver (GGIK) that is able to produce a large number of diverse solutions in parallel while also generalizing well -- a single learned model can be used to produce IK solutions for a variety of different robots. The graphical formulation elegantly exposes the symmetry and Euclidean equivariance of the IK problem that stems from the spatial nature of robot manipulators. We exploit this symmetry by encoding it into the architecture of our learned model, yielding a flexible solver that is able to produce sets of IK solutions for multiple robots.

One Network, Many Robots: Generative Graphical Inverse Kinematics

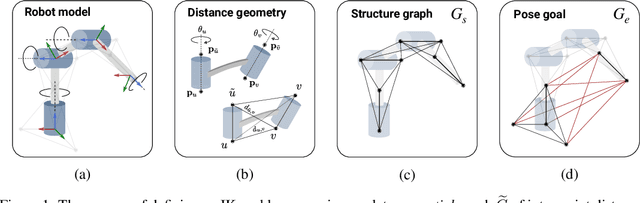
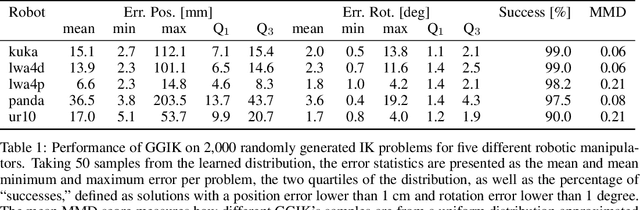
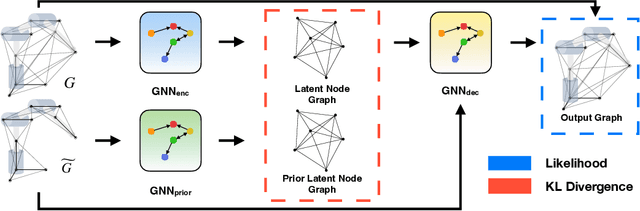
Quickly and reliably finding accurate inverse kinematics (IK) solutions remains a challenging problem for robotic manipulation. Existing numerical solvers are broadly applicable, but rely on local search techniques to manage highly nonconvex objective functions. Recently, learning-based approaches have shown promise as a means to generate fast and accurate IK results; learned solvers can easily be integrated with other learning algorithms in end-to-end systems. However, learning-based methods have an Achilles' heel: each robot of interest requires a specialized model which must be trained from scratch. To address this key shortcoming, we investigate a novel distance-geometric robot representation coupled with a graph structure that allows us to leverage the flexibility of graph neural networks (GNNs). We use this approach to train the first learned generative graphical inverse kinematics (GGIK) solver that is, crucially, "robot-agnostic"-a single model is able to provide IK solutions for a variety of different robots. Additionally, the generative nature of GGIK allows the solver to produce a large number of diverse solutions in parallel with minimal additional computation time, making it appropriate for applications such as sampling-based motion planning. Finally, GGIK can complement local IK solvers by providing reliable initializations. These advantages, as well as the ability to use task-relevant priors and to continuously improve with new data, suggest that GGIK has the potential to be a key component of flexible, learning-based robotic manipulation systems.