Evaluation of uncertainty estimations for Gaussian process regression based machine learning interatomic potentials

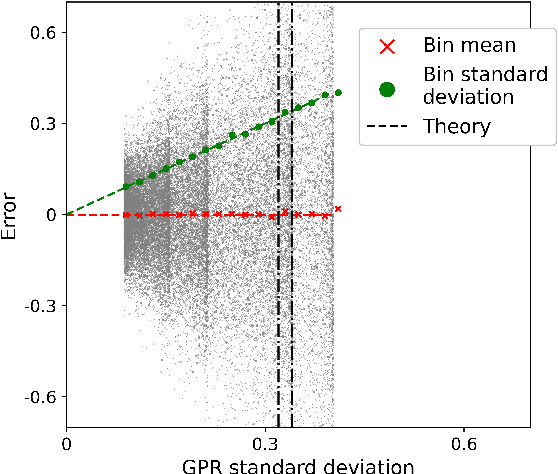
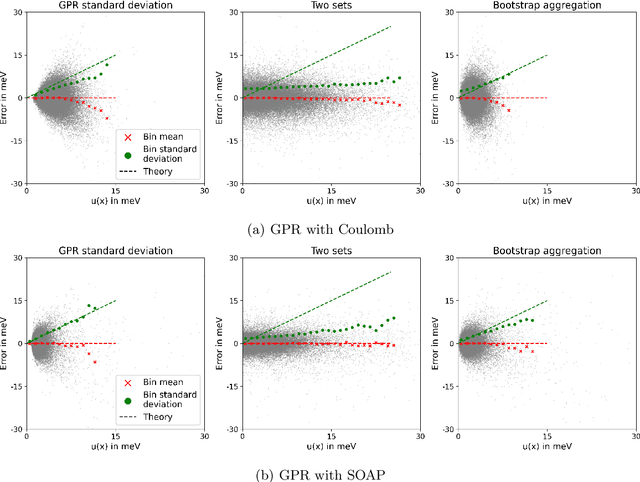
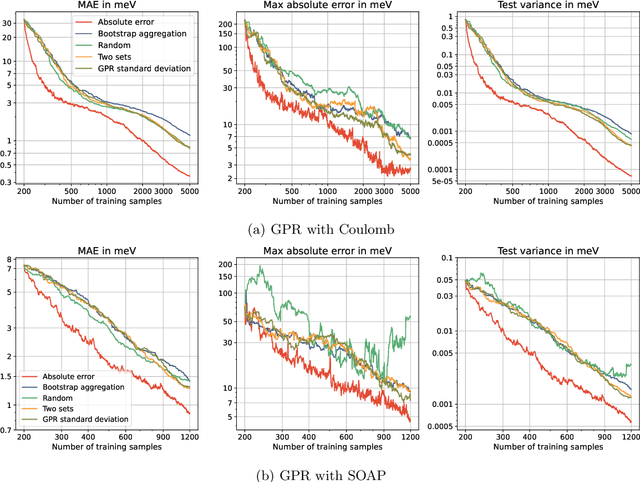
Machine learning interatomic potentials (MLIPs) have seen significant advances as efficient replacement of expensive quantum chemical calculations. Uncertainty estimations for MLIPs are crucial to quantify the additional model error they introduce and to leverage this information in active learning strategies. MLIPs that are based on Gaussian process regression provide a standard deviation as a possible uncertainty measure. An alternative approach are ensemble-based uncertainties. Although these uncertainty measures have been applied to active learning, it has rarely been studied how they correlate with the error, and it is not always clear whether active learning actually outperforms random sampling strategies. We consider GPR models with Coulomb and SOAP representations as inputs to predict potential energy surfaces and excitation energies of molecules. We evaluate, how the GPR variance and ensemble-based uncertainties relate to the error and whether model performance improves by selecting the most uncertain samples from a fixed configuration space. For the ensemble based uncertainty estimations, we find that they often do not provide any information about the error. For the GPR standard deviation, we find that often predictions with an increasing standard deviation also have an increasing systematical bias, which is not captured by the uncertainty. In these cases, selecting training samples with the highest uncertainty leads to a model with a worse test error compared to random sampling. We conclude that confidence intervals, which are derived from the predictive standard deviation, can be highly overconfident. Selecting samples with high GPR standard deviation leads to a model that overemphasizes the borders of the configuration space represented in the fixed dataset. This may result in worse performance in more densely sampled areas but better generalization for extrapolation tasks.

Investigating Data Hierarchies in Multifidelity Machine Learning for Excitation Energies

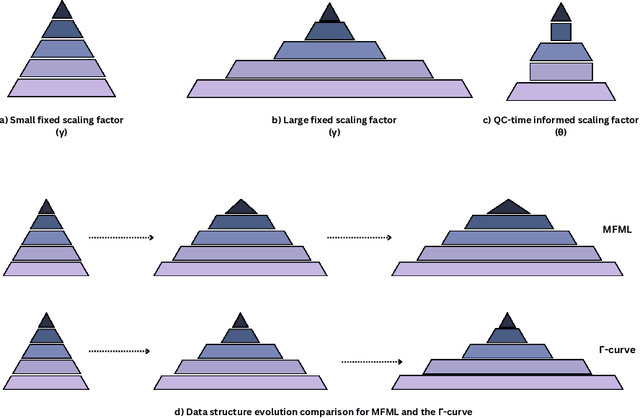
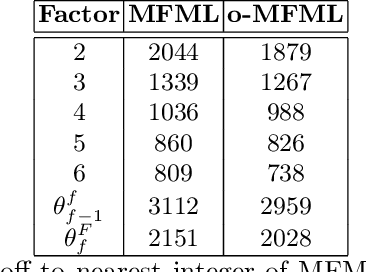
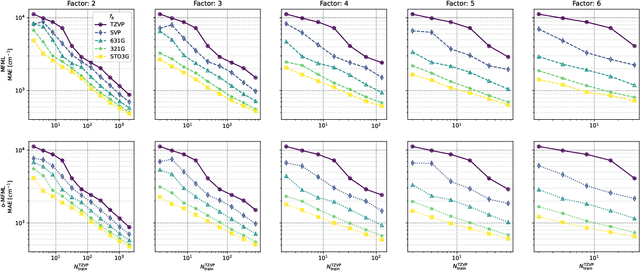
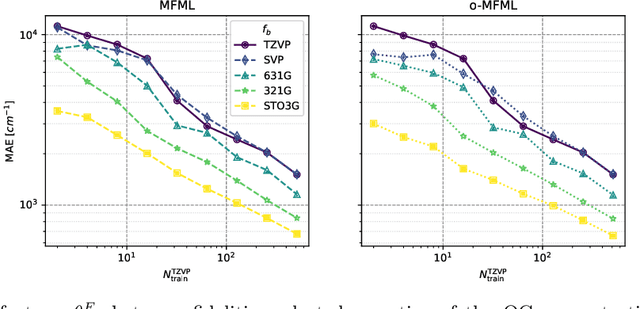
Recent progress in machine learning (ML) has made high-accuracy quantum chemistry (QC) calculations more accessible. Of particular interest are multifidelity machine learning (MFML) methods where training data from differing accuracies or fidelities are used. These methods usually employ a fixed scaling factor, $\gamma$, to relate the number of training samples across different fidelities, which reflects the cost and assumed sparsity of the data. This study investigates the impact of modifying $\gamma$ on model efficiency and accuracy for the prediction of vertical excitation energies using the QeMFi benchmark dataset. Further, this work introduces QC compute time informed scaling factors, denoted as $\theta$, that vary based on QC compute times at different fidelities. A novel error metric, error contours of MFML, is proposed to provide a comprehensive view of model error contributions from each fidelity. The results indicate that high model accuracy can be achieved with just 2 training samples at the target fidelity when a larger number of samples from lower fidelities are used. This is further illustrated through a novel concept, the $\Gamma$-curve, which compares model error against the time-cost of generating training samples, demonstrating that multifidelity models can achieve high accuracy while minimizing training data costs.

Benchmarking Data Efficiency in $Δ$-ML and Multifidelity Models for Quantum Chemistry

The development of machine learning (ML) methods has made quantum chemistry (QC) calculations more accessible by reducing the compute cost incurred in conventional QC methods. This has since been translated into the overhead cost of generating training data. Increased work in reducing the cost of generating training data resulted in the development of $\Delta$-ML and multifidelity machine learning methods which use data at more than one QC level of accuracy, or fidelity. This work compares the data costs associated with $\Delta$-ML, multifidelity machine learning (MFML), and optimized MFML (o-MFML) in contrast with a newly introduced Multifidelity$\Delta$-Machine Learning (MF$\Delta$ML) method for the prediction of ground state energies over the multifidelity benchmark dataset QeMFi. This assessment is made on the basis of training data generation cost associated with each model and is compared with the single fidelity kernel ridge regression (KRR) case. The results indicate that the use of multifidelity methods surpasses the standard $\Delta$-ML approaches in cases of a large number of predictions. For cases, where $\Delta$-ML method might be favored, such as small test set regimes, the MF$\Delta$-ML method is shown to be more efficient than conventional $\Delta$-ML.

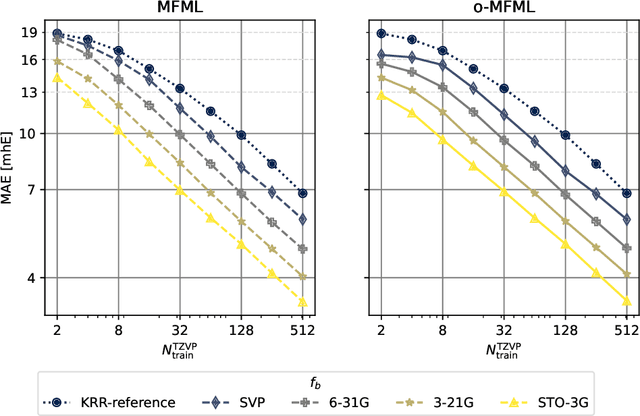
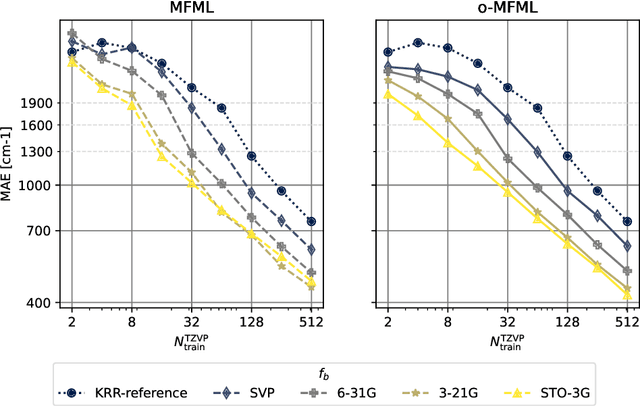
Assessing Non-Nested Configurations of Multifidelity Machine Learning for Quantum-Chemical Properties

Multifidelity machine learning (MFML) for quantum chemical (QC) properties has seen strong development in the recent years. The method has been shown to reduce the cost of generating training data for high-accuracy low-cost ML models. In such a set-up, the ML models are trained on molecular geometries and some property of interest computed at various computational chemistry accuracies, or fidelities. These are then combined in training the MFML models. In some multifidelity models, the training data is required to be nested, that is the same molecular geometries are included to calculate the property across all the fidelities. In these multifidelity models, the requirement of a nested configuration restricts the kind of sampling that can be performed while selection training samples at different fidelities. This work assesses the use of non-nested training data for two of these multifidelity methods, namely MFML and optimized MFML (o-MFML). The assessment is carried out for the prediction of ground state energies and first vertical excitation energies of a diverse collection of molecules of the CheMFi dataset. Results indicate that the MFML method still requires a nested structure of training data across the fidelities. However, the o-MFML method shows promising results for non-nested multifidelity training data with model errors comparable to the nested configurations.

Data-driven identification of port-Hamiltonian DAE systems by Gaussian processes

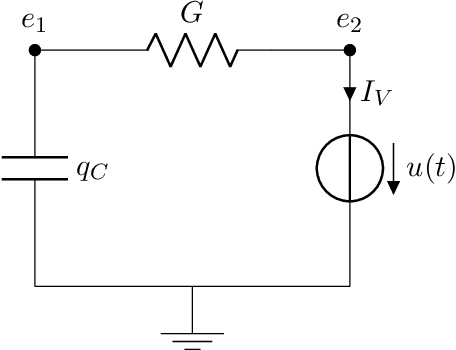
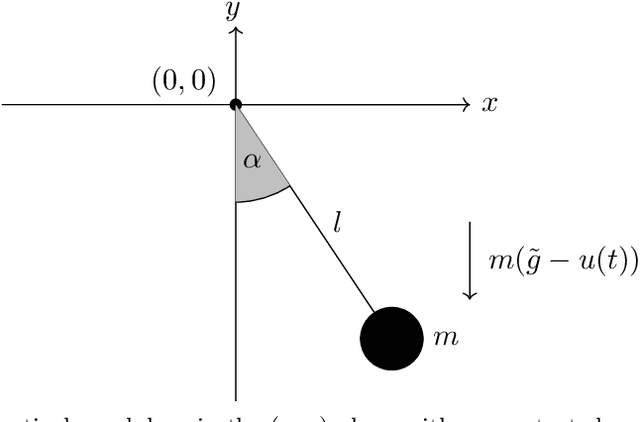
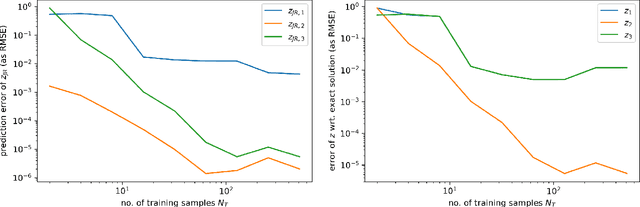
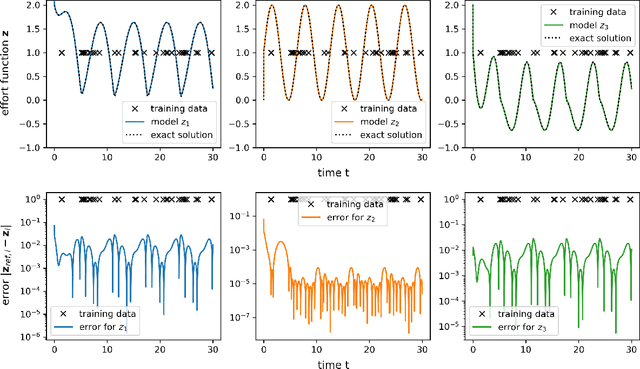
Port-Hamiltonian systems (pHS) allow for a structure-preserving modeling of dynamical systems. Coupling pHS via linear relations between input and output defines an overall pHS, which is structure preserving. However, in multiphysics applications, some subsystems do not allow for a physical pHS description, as (a) this is not available or (b) too expensive. Here, data-driven approaches can be used to deliver a pHS for such subsystems, which can then be coupled to the other subsystems in a structure-preserving way. In this work, we derive a data-driven identification approach for port-Hamiltonian differential algebraic equation (DAE) systems. The approach uses input and state space data to estimate nonlinear effort functions of pH-DAEs. As underlying technique, we us (multi-task) Gaussian processes. This work thereby extends over the current state of the art, in which only port-Hamiltonian ordinary differential equation systems could be identified via Gaussian processes. We apply this approach successfully to two applications from network design and constrained multibody system dynamics, based on pH-DAE system of index one and three, respectively.

CheMFi: A Multifidelity Dataset of Quantum Chemical Properties of Diverse Molecules

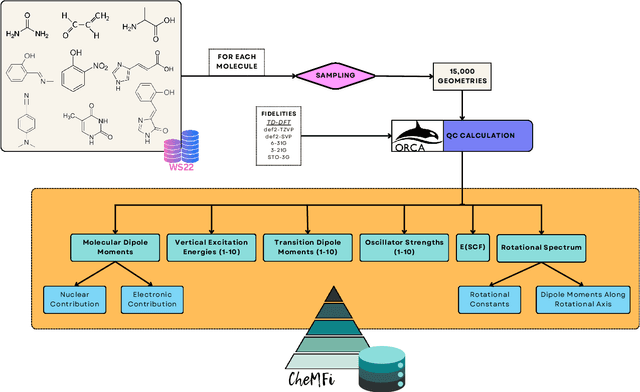
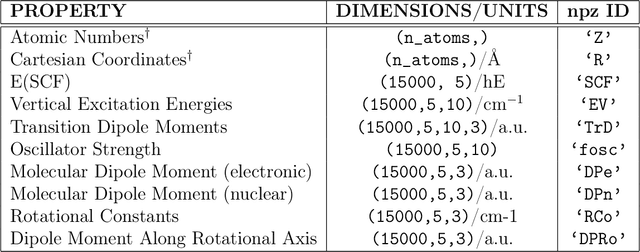
Progress in both Machine Learning (ML) and conventional Quantum Chemistry (QC) computational methods have resulted in high accuracy ML models for QC properties ranging from atomization energies to excitation energies. Various datasets such as MD17, MD22, and WS22, which consist of properties calculated at some level of QC method, or fidelity, have been generated to benchmark such ML models. The term fidelity refers to the accuracy of the chosen QC method to the actual real value of the property. The higher the fidelity, the more accurate the calculated property, albeit at a higher computational cost. Research in multifidelity ML (MFML) methods, where ML models are trained on data from more than one numerical QC method, has shown the effectiveness of such models over single fidelity methods. Much research is progressing in this direction for diverse applications ranging from energy band gaps to excitation energies. A major hurdle for effective research in this field of research in the community is the lack of a diverse multifidelity dataset for benchmarking. Here, we present a comprehensive multifidelity dataset drawn from the WS22 molecular conformations. We provide the quantum Chemistry MultiFidelity (CheMFi) dataset consisting of five fidelities calculated with the TD-DFT formalism. The fidelities differ in their basis set choice and are namely: STO-3G, 3-21G, 6-31G, def2-SVP, and def2-TZVP. CheMFi offers to the community a variety of QC properties including vertical excitation energies, oscillator strengths, molecular dipole moments, and ground state energies. In addition to the dataset, multifidelity benchmarks are set with state-of-the-art MFML and optimized-MFML

Multi-Fidelity Machine Learning for Excited State Energies of Molecules

The accurate but fast calculation of molecular excited states is still a very challenging topic. For many applications, detailed knowledge of the energy funnel in larger molecular aggregates is of key importance requiring highly accurate excited state energies. To this end, machine learning techniques can be an extremely useful tool though the cost of generating highly accurate training datasets still remains a severe challenge. To overcome this hurdle, this work proposes the use of multi-fidelity machine learning where very little training data from high accuracies is combined with cheaper and less accurate data to achieve the accuracy of the costlier level. In the present study, the approach is employed to predict the first excited state energies for three molecules of increasing size, namely, benzene, naphthalene, and anthracene. The energies are trained and tested for conformations stemming from classical molecular dynamics simulations and from real-time density functional tight-binding calculations. It can be shown that the multi-fidelity machine learning model can achieve the same accuracy as a machine learning model built only on high cost training data while having a much lower computational effort to generate the data. The numerical gain observed in these benchmark test calculations was over a factor of 30 but certainly can be much higher for high accuracy data.

Towards data-driven filters in Paraview

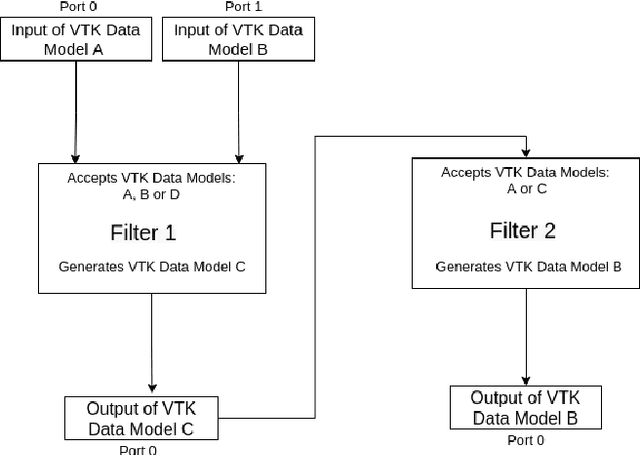
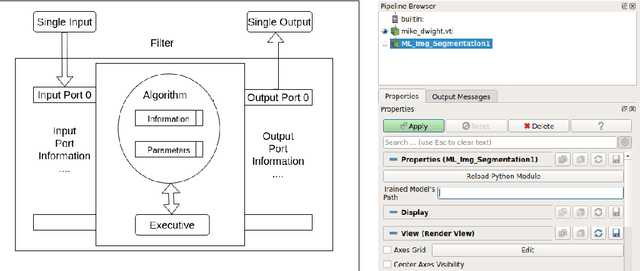
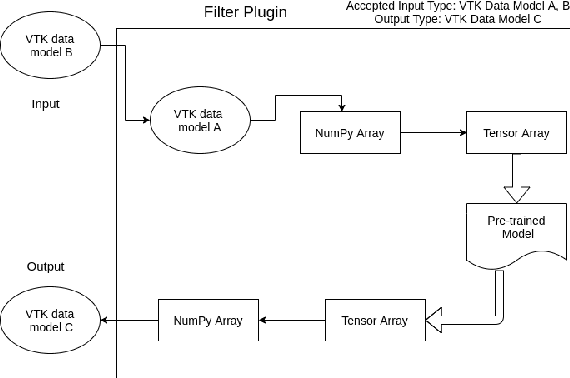
Recent progress in scientific visualization has expanded the scope of visualization from being merely a way of presentation to an analysis and discovery tool. A given visualization result is usually generated by applying a series of transformations or filters to the underlying data. Nowadays, such filters use deterministic algorithms to process the data. In this work, we aim at extending this methodology towards data-driven filters, thus filters that expose the abilities of pre-trained machine learning models to the visualization system. The use of such data-driven filters is of particular interest in fields like segmentation, classification, etc., where machine learning models regularly outperform existing algorithmic approaches. To showcase this idea, we couple Paraview, the well-known flow visualization tool, with PyTorch, a deep learning framework. Paraview is extended by plugins that allow users to load pre-trained models of their choice in the form of newly developed filters. The filters transform the input data by feeding it into the model and then provide the model's output as input to the remaining visualization pipeline. A series of simplistic use cases for segmentation and classification on image and fluid data is presented to showcase the technical applicability of such data-driven transformations in Paraview for future complex analysis tasks.