Evaluation of uncertainty estimations for Gaussian process regression based machine learning interatomic potentials

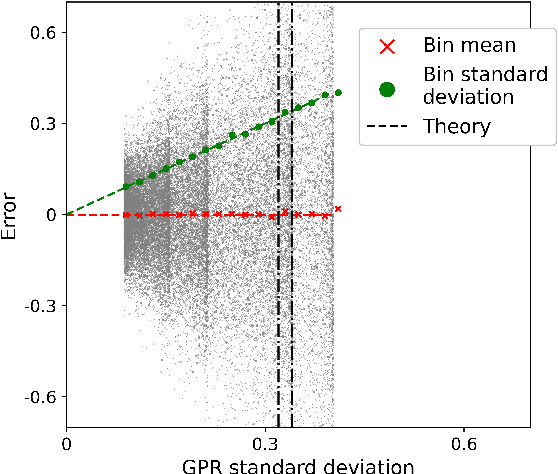
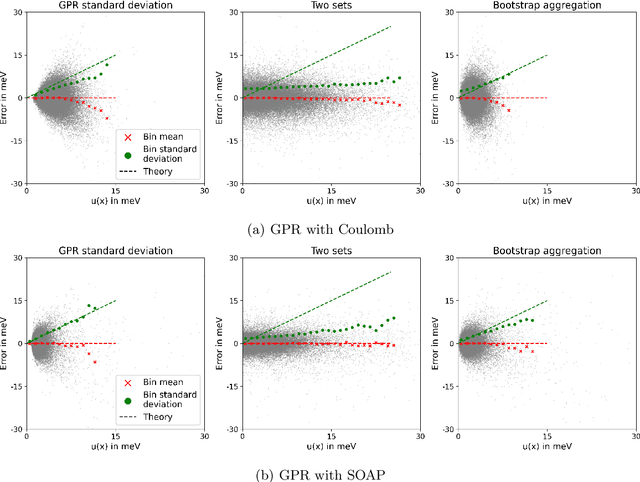
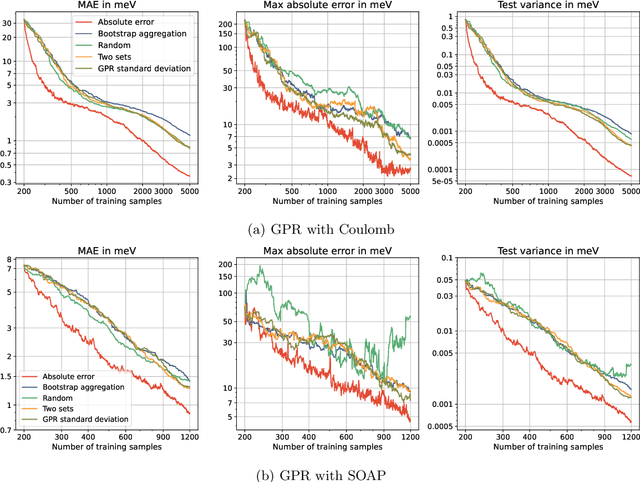
Machine learning interatomic potentials (MLIPs) have seen significant advances as efficient replacement of expensive quantum chemical calculations. Uncertainty estimations for MLIPs are crucial to quantify the additional model error they introduce and to leverage this information in active learning strategies. MLIPs that are based on Gaussian process regression provide a standard deviation as a possible uncertainty measure. An alternative approach are ensemble-based uncertainties. Although these uncertainty measures have been applied to active learning, it has rarely been studied how they correlate with the error, and it is not always clear whether active learning actually outperforms random sampling strategies. We consider GPR models with Coulomb and SOAP representations as inputs to predict potential energy surfaces and excitation energies of molecules. We evaluate, how the GPR variance and ensemble-based uncertainties relate to the error and whether model performance improves by selecting the most uncertain samples from a fixed configuration space. For the ensemble based uncertainty estimations, we find that they often do not provide any information about the error. For the GPR standard deviation, we find that often predictions with an increasing standard deviation also have an increasing systematical bias, which is not captured by the uncertainty. In these cases, selecting training samples with the highest uncertainty leads to a model with a worse test error compared to random sampling. We conclude that confidence intervals, which are derived from the predictive standard deviation, can be highly overconfident. Selecting samples with high GPR standard deviation leads to a model that overemphasizes the borders of the configuration space represented in the fixed dataset. This may result in worse performance in more densely sampled areas but better generalization for extrapolation tasks.

Spectral Densities, Structured Noise and Ensemble Averaging within Open Quantum Dynamics

Although recent advances in simulating open quantum systems have lead to significant progress, the applicability of numerically exact methods is still restricted to rather small systems. Hence, more approximate methods remain relevant due to their computational efficiency, enabling simulations of larger systems over extended timescales. In this study, we present advances for one such method, namely the Numerical Integration of Schr\"odinger Equation (NISE). Firstly, we introduce a modified ensemble-averaging procedure that improves the long-time behavior of the thermalized variant of the NISE scheme, termed Thermalized NISE. Secondly, we demonstrate how to use the NISE in conjunction with (highly) structured spectral densities by utilizing a noise generating algorithm for arbitrary structured noise. This algorithm also serves as a tool for establishing best practices in determining spectral densities from excited state calculations along molecular dynamics or quantum mechanics/molecular mechanics trajectories. Finally, we assess the ability of the NISE approach to calculate absorption spectra and demonstrate the utility of the proposed modifications by determining population dynamics.

Multi-Fidelity Machine Learning for Excited State Energies of Molecules

The accurate but fast calculation of molecular excited states is still a very challenging topic. For many applications, detailed knowledge of the energy funnel in larger molecular aggregates is of key importance requiring highly accurate excited state energies. To this end, machine learning techniques can be an extremely useful tool though the cost of generating highly accurate training datasets still remains a severe challenge. To overcome this hurdle, this work proposes the use of multi-fidelity machine learning where very little training data from high accuracies is combined with cheaper and less accurate data to achieve the accuracy of the costlier level. In the present study, the approach is employed to predict the first excited state energies for three molecules of increasing size, namely, benzene, naphthalene, and anthracene. The energies are trained and tested for conformations stemming from classical molecular dynamics simulations and from real-time density functional tight-binding calculations. It can be shown that the multi-fidelity machine learning model can achieve the same accuracy as a machine learning model built only on high cost training data while having a much lower computational effort to generate the data. The numerical gain observed in these benchmark test calculations was over a factor of 30 but certainly can be much higher for high accuracy data.