Data-driven identification of port-Hamiltonian DAE systems by Gaussian processes
Paper and Code
Jun 26, 2024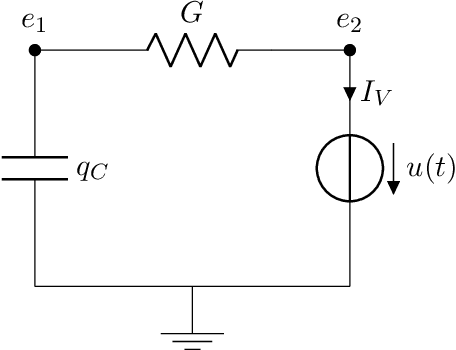
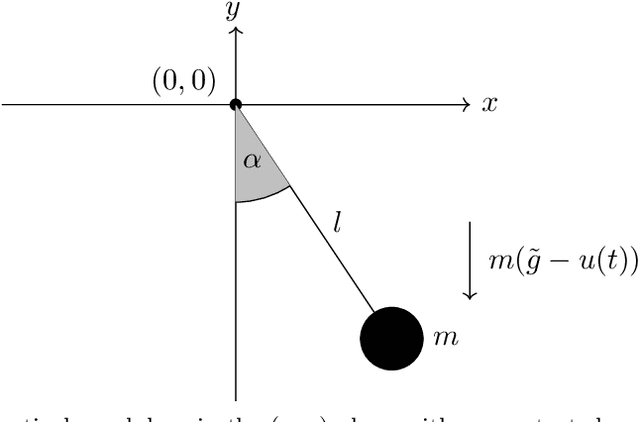
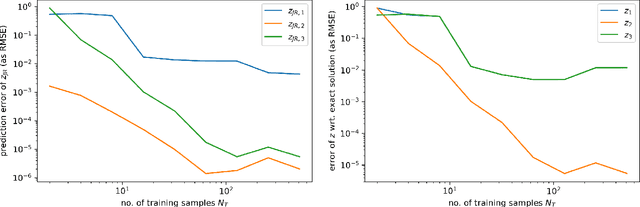
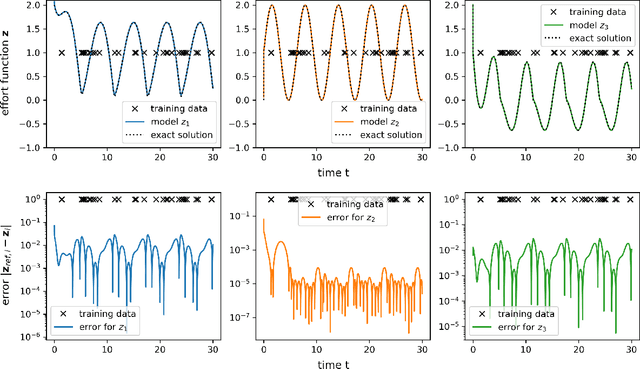
Port-Hamiltonian systems (pHS) allow for a structure-preserving modeling of dynamical systems. Coupling pHS via linear relations between input and output defines an overall pHS, which is structure preserving. However, in multiphysics applications, some subsystems do not allow for a physical pHS description, as (a) this is not available or (b) too expensive. Here, data-driven approaches can be used to deliver a pHS for such subsystems, which can then be coupled to the other subsystems in a structure-preserving way. In this work, we derive a data-driven identification approach for port-Hamiltonian differential algebraic equation (DAE) systems. The approach uses input and state space data to estimate nonlinear effort functions of pH-DAEs. As underlying technique, we us (multi-task) Gaussian processes. This work thereby extends over the current state of the art, in which only port-Hamiltonian ordinary differential equation systems could be identified via Gaussian processes. We apply this approach successfully to two applications from network design and constrained multibody system dynamics, based on pH-DAE system of index one and three, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge