Learning Robust Decision Policies from Observational Data

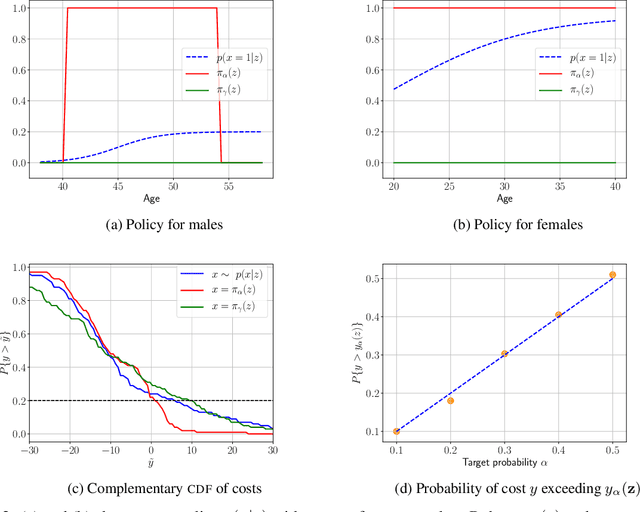
We address the problem of learning a decision policy from observational data of past decisions in contexts with features and associated outcomes. The past policy maybe unknown and in safety-critical applications, such as medical decision support, it is of interest to learn robust policies that reduce the risk of outcomes with high costs. In this paper, we develop a method for learning policies that reduce tails of the cost distribution at a specified level and, moreover, provide a statistically valid bound on the cost of each decision. These properties are valid under finite samples -- even in scenarios with uneven or no overlap between features for different decisions in the observed data -- by building on recent results in conformal prediction. The performance and statistical properties of the proposed method are illustrated using both real and synthetic data.

Robust Risk Minimization for Statistical Learning

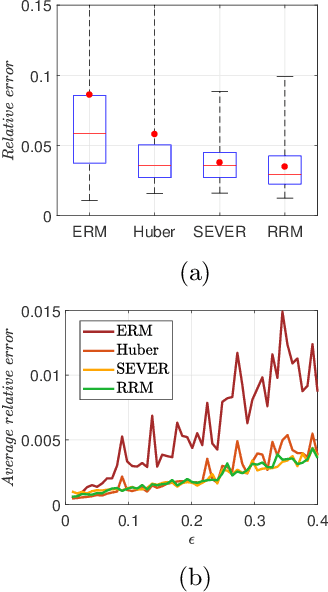
We consider a general statistical learning problem where an unknown fraction of the training data is corrupted. We develop a robust learning method that only requires specifying an upper bound on the corrupted data fraction. The method is formulated as a risk minimization problem that can be solved using a blockwise coordinate descent algorithm. We demonstrate the wide range applicability of the method, including regression, classification, unsupervised learning and classic parameter estimation, with state-of-the-art performance.